Übungsblatt 4
Zeitpropagation
Anmerkung: Die Abgabe von Arbeitsblatt 1 bis 4 ist verpflichtend und konstituiert die Studienleistung der Veranstaltung Simulationstechniken. Die Arbeitsblätter führen von der mathematischen Formulierung eines Modellproblems hin zur numerischen Lösung dieses Problems und bauen aufeinander auf. Zum Bestehen der Veranstaltung müssen auf jedem Blatt mindestens 50% der erzielbaren Punkte erreicht werden.
Geben Sie bei allen Aufgaben die Lösungswege und Zwischenergebnisse mit an. Das Endergebnis alleine ist nicht ausreichend! Wir empfehlen Ihnen die Nutzung von Python. Sollten Sie ein Jupyter-Notebook verwenden, dann können Sie dieses einfach direkt als Lösung bei uns einreichen. In allen anderen Fällen erzeugen Sie bitte ein PDF und legen die numerischen Codes als separate Datei dazu.
Sie werden durch die einzelnen Schritte der Modellimplementierung geleitet, und wir geben Hinweise zur Implementierung. Es ist nicht zwingend notwendig, diese 1-zu-1 zu verfolgen. Im Rahmen dieser Hinweise finden Sie Codeabschnitte, die Sie verwenden können. Sie dürfen natürlich auch die Codebeispiele aus dem Vorlesungsmaterial hier verwenden.
4.1 Zeitpropagation der Poisson-Nernst-Planck-Gleichung: Einführung
0 Punkte
Die (nichtlineare) Poisson-Boltzmann-Gleichung entspricht der Poisson-Nernst-Planck (PNP) Gleichungen im thermodynamischen Gleichgewicht. Falls die Ionenstromdichte nicht verschwindet, müssen wir die Poisson-Nernst-Planck-Gleichungen betrachten. Wir betrachten hier die in Übungsblatt 3, Aufgabe 1 hergeleitete entdimensionalisierte Variante dieser Gleichung. Nutzen Sie im folgenden zwei Ionenspezies \(\alpha =+\) und \(\alpha =-\), mit den (entdimensionalisierten) Ladungen \(q_+=+1\) und \(q_-=-1\).
In dieser Aufgabe wollen wir uns für ein eindimensionales Problem die zeitliche Entwicklung der Ionenkonzentrationen nach einem gegebenen Anfangszustand anschauen. Die Anwendung, welche wir hier diskutieren, ist ein elektrochemischer Kondensator mit zwei parallelen Platten. Durch die Lösung der PNP Gleichungen erhalten wir hier die Ladung als eine Funktion des Potentials. Da diese Lösung die komplette zeitliche Entwicklung der Ionenkonzentration beschreibt, können wir nun auch schauen, wir sich das System bei einer Anregung verhält, die sich zeitlich ändert. Hiermit werden wir in der Lage sein, Strom-Spannungskennlinien zu berechnen. In der Elektrochemie werden solche Kennlinien oft in Form von Cylcovoltammogrammen aufgenommen. Die hier berechneten Cyclovoltammogramme werden keine Faradayschen Prozesse, also chemische Reaktion an der Elektrode, berücksichtigen, beschreiben aber die Dynamik der Ladungsumordnung.
Für gegebene Randbedingungen und Anfangskonzentrationen \(c_s(x, t=0)\) wollen wir die Konzentrationen \(c_s(x, t)\) berechnen. Dafür werden wir die Nernst-Planck Gleichung mithilfe des Runge-Kutta-Verfahrens zeitlich integrieren. Aber zunächst wollen wir uns mit der räumlichen Diskretisierung mittels der Finite-Elemente-Methode (FEM) beschäftigen.
4.2 Diskretisierung mit Hilfe der finite-Elemente Methode
6 Punkte
Benutzen Sie die FEM um die PNP Gleichungen in ein Gleichungssystem in \(\dot c_{\alpha i}\), \(c_{\alpha i}\) und \(\Phi _{j}\) zu Überführen. Benutzen Sie hierfür eindimensionale lineare Basisfunktionen. Die Ansatzfunktionen haben nun zeitabhängige Entwicklungskoeffizienten, \begin {align} c_\alpha (x, t) &= \sum _i c_{\alpha i}(t) \varphi _i(x) \\ \Phi (x, t) &= \sum _j \Phi _j(t) \varphi _j(x), \end {align}
und wir nutzen die gleiche Basis für alle drei Felder.
Diese drei konstituierenden Gleichungen können einzeln diskretisiert werden. Sie koppeln über das elektrostatische Potential \(\Phi \). An den Rändern mit Neumann-Randbedingungen werden Gradienten oder Flüße in den hier betrachteten Beispielen immer verschwinden, d.h. Sie können die entsprechenden Terme frühzeitig auslassen. Bitte arbeiten Sie ab hier mit der eindimensionalen Variante der PNP-Gleichungen. Rechnen Sie die Integrale zunächst nicht explizit aus, aber ersetzen Sie diese durch Symbole.
Sie sollten ein System der Form \begin {align} \label {eq:pnp-discrete-system-1-p} \sum _j L_{ij} \Phi _j &= \frac {1}{2} \sum _j M_{ij}\left (q_+c_{+j} + q_-c_{-j}\right ) \\ \sum _j M_{ij} \dot c_{\alpha j} &= -\sum _j L_{ij} c_{\alpha j} - q_\alpha \sum _{jk} C_{ijk} c_{\alpha j} \Phi _k \label {eq:pnp-discrete-system-1-np} \end {align}
erhalten. Wir haben hier die homogenen Neumann-Terme weggelassen. Welche Schwierigkeiten erwarten Sie?
4.3 Berechnung der Basisfunktionsintegrale
6 Punkte
Bitte verwenden Sie nun ein reguläres Gitter (konstanter Abstand \(\Delta x\)) mit linearen finiten Elementen wie in der Vorlesung vorgestellt. Rechnen Sie nun die Integrale \(L_{ij}\), \(M_{ij}\) und \(C_{ijk}\) explizit aus. Einige dieser Integrale sind schon in der Vorlesung und auf vorherigen Übungsblättern aufgetaucht. Zum Berechnen der Integrale können Sie natürlich ein Computeralgebrasystem (wie z.B. Mathematica oder sympy) benutzen.
Achtung: Beachten Sie, dass die Integrale am Rand des Gebiets anders aussehen als in der Mitte.
4.4 Implementierung der Gleichungssysteme
0 Punkte
Implementieren Sie nun die linken und rechten Seiten der Gleichungen \eqref{eq:pnp-discrete-system-1-p} und \eqref{eq:pnp-discrete-system-1-np}. Wir schlagen die unten genannten Funktionsnamen und Funktionssignaturen vor.
Anmerkung: Sie brauchen einige der auftretenden Matrizen nicht explizit berechnen. Beispielsweise können Sie anstelle \(\underline {C}\) konkret aufzustellen, auch nur die Auswirkung von \(\underline {C}\) auf einen Vektor implementieren. Dies führt zu erheblich kompakterem Code. Der Grund dafür ist, dass wir bei der expliziten Zeitpropagation im Gegensatz zu den vorher behandelten ˙impliziten˙ Methoden nicht explizit ein lineares Gleichungssystem lösen müssen. (Achtung: \(\underline {M}\) müssen Sie explizit als Matrix berechnen! Für die Lösung der Poisson-Gleichung brauchen Sie auch \(\underline {L}\) explizit als Matrix!)
2 """
3 Return the Laplace operator L_{ij}
4
5 Parameters
6 ----------
7 nb_nodes : int
8 Number of nodes
9 dx : float
10 Grid spacing
11
12 Returns
13 -------
14 laplacian_gg : np.ndarray of shape (nb_nodes, nb_nodes)
15 Matrix containing the laplacian matrix
16 """
17 pass
18
19def massian(nb_nodes, dx):
20 """
21 Return the mass matrix M_{ij}
22
23 Parameters
24 ----------
25 nb_nodes : int
26 Number of nodes
27 dx : float
28 Grid spacing
29
30 Returns
31 -------
32 massian_gg : np.ndarray of shape (nb_nodes, nb_nodes)
33 Matrix containing the mass matrix
34 """
35 pass
36
37def apply_C(concentration_g, potential_g, dx):
38 r"""
39 Implements the term
40
41 C_{ijk} c_{\alpha j} \Phi_k
42
43 Parameters
44 ----------
45 concentration_g : np.ndarray of shape (nb_nodes,)
46 Concentration
47 potential_g : ndarray of shape (nb_nodes,)
48 Electrostatic potential
49 dx : float
50 Grid spacing
51
52 Returns
53 -------
54 C_g : np.ndarray of shape (nb_nodes,)
55 Drift term of the drift diffusion equation
56 """
57 pass
58
59def compute_potential(charge_density_g, dx, potential_left=0, potential_right=0,
60 massian_gg=None):
61 """
62 Solve the Poisson equation to compute the electrostatic potential
63
64 Parameters
65 ----------
66 charge_density_g : np.ndarray of shape (nb_nodes,)
67 Charge density
68 dx : float
69 Grid spacing
70 potential_left : float, optional
71 Potential of the left electrode
72 (Default: 0)
73 potential_right : float, optional
74 Potential of the right electrode
75 (Default: 0)
76 massian_gg : np.ndarray of shape (nb_nodes, nb_nodes)
77 Matrix containing the Massian. Recompute if None
78 (Default: None)
79
80 Returns
81 -------
82 potential_g : np.ndarray of shape (nb_nodes,)
83 Electric potential on the nodes
84 """
85 pass
86
87def drift_diffusion_rhs(concentration_g, potential_g, charge, dx,
88 laplacian_gg=None):
89 r"""
90 Implements the term
91
92 L_{ij} c_{\alpha j} + q_\alpha C_{ijk} c_{\alpha j} \Phi_k
93
94 Parameters
95 ----------
96 concentration_g : np.ndarray of shape (nb_nodes,)
97 Concentration of the species
98 potential_g : ndarray of shape (nb_nodes,)
99 Electrostatic potential
100 charge : float
101 Charge of the species
102 dx : float
103 Grid spacing
104 laplacian_gg : np.ndarray of shape (nb_nodes, nb_nodes)
105 Matrix containing the Laplace operator. Recompute if None
106 (Default: None)
107
108 Returns
109 -------
110 rhs_g : np.ndarray of shape (nb_nodes,)
111 Right hand side (source term) for the Drift-Diffusion equation
112 """
113 pass
4.5 Zeitliche Integration
2 Punkte
Die diskretisierten Nernst-Planck-Gleichungen bilden ein System gewöhnlicher Differenzialgleichungen erster Ordnung in \(c\), wobei \(\Phi _k\) die Lösung der Poisson-Gleichung ist, die in jedem Zeitschritt neu berechnet werden muss. Benutzen Sie scipy.integrate.solve_ivp um die PNP-Gleichungen zeitlich zu integrieren. solve_ivp löst das System von GDGLs mit unterschiedlichen Verfahren, die mit dem Parameter method ausgewählt werden können. Die Standardintegrationsmethode ist ein Runge-Kutta-Verfahren mit adaptivem Zeitschritt (RK45), die gut funktionieren sollte.
solve_ivp benötigt eine Funktion pnp_dcdt(time, concentration_flat), die die zeitliche Ableitung \(\frac {\mathrm {d}c}{\mathrm {d}t}\) berechnet. Beachten Sie, dass diese Funktion einen ”flachenÄrray als Input benötigt.
solve_ivp entscheidet selbst, welcher Zeitschritt für eine stabile Zeitintegration nötig ist. Dafür muss angegeben werden, an welchen Zeitpunkten die Konzentration ausgewertet werden soll. Die Zeitschritte, bei denen die Konzentration ausgegeben werden sollen, werden durch t_eval festgelegt.
Im folgenden finden Sie einen Vorschlag, wie die Signatur einer Funktion, die Ihre PNP-Gleichung propagiert, aussehen könnte.
2 initial_concentration_n_g,
3 dx,
4 maximum_time,
5 nb_output=2,
6 potential_left=0,
7 potential_right=0,
8 positive_charge=1,
9 negative_charge=-1,
10 **kwargs):
11 """
12 Integrate the Poisson-Nernst-Planck equation forward in time from a starting
13 configuration.
14
15 Parameters
16 ----------
17 initial_concentration_p_g : numpy.ndarray of shape (nb_nodes,)
18 Initial concentration of the positively charges species
19 initial_concentration_n_g : numpy.ndarray of shape (nb_nodes,)
20 Initial concentration of the negatively charges species
21 dx : float
22 Grid spacing
23 maximum_time : float
24 Integrate from time 0 up to this time
25 nb_output : int, optional
26 Frequency of output time steps
27 (Default: 2)
28 potential_left : float, optional
29 Potential of the left electrode
30 (Default: 0)
31 potential_right : float, optional
32 Potential of the right electrode
33 (Default: 0)
34 positive_charge : float, optional
35 Charge of positive species
36 (Default: +1)
37 negative_charge : float, optional
38 Charge of negative species
39 (Default: -1)
40
41 Returns
42 -------
43 time_t : numpy.ndarray of shape (nb_nodes,)
44 Times at which the output is reported
45 concentration_p_tg : ndarray of shape (nb_output, nb_nodes)
46 Concentration of the positive species at certain times
47 concentration_n_tg : ndarray of shape (nb_output, nb_nodes)
48 Concentration of the negative species at certain times
49 """
50 pass
4.6 Systematische Tests der Implementierung
Um sicherzustellen, dass die Implementation korrekt ist, werden wir erstmal einfache Sonderfälle betrachten. Dabei steigert sich die Komplexität Schritt für Schritt. Sie können so schon einen Teil des Codes testen, bevor alles implementiert ist.
4.6.1 Nernst-Planck-Gleichung mit \(q_\alpha =0\), die Diffusionsgleichung
2 Punkte
Wir betrachten nur eine Spezies, die Ladungsneutral ist. Damit wird die Poisson-Nernst-Planck-Gleichung zur altbekannten Diffusionsgleichung:
Eine Spezies
Durch die Ränder des Simulationsgebiets fließt kein Stoff, d.h. wir betrachten homogene Neumann-Randbedingungen. Vergewissern Sie sich, dass \(c(x, t) = c^\infty + \Delta c \exp \left [-D\left (\frac {2\pi }{L}\right )^2 t \right ] \cos (2 \pi x /L)\) für eine Initialverteilung \(c(x, 0) = c^\infty + \Delta c \cos (2 \pi x /L)\) und benannte Randbedingungen eine Lösung der Diffusionsgleichung \(\dot c = D \frac {\partial ^2 c}{\partial x ^ 2}\) ist. Achten Sie darauf, dass \(\Delta c < c^\infty \). (Warum ist das wichtig?)
Zeigen Sie, dass Ihr Modell mit der analytischen Lösung der Diffusionsgleichung übereinstimmt. Stellen Sie dafür die analytische Lösung und einen Schnitt der numerischen Lösung bei den Zeitschritten \(t = 0.\), \(t=0.05\) und \(t=0.1\) dar. Verwenden Sie dabei einen Plattenabstand von \(L=2\).
Anmerkung: Auf Grund der CFL-Bedindung benötigen feinere Gitter kleinere Zeitschritte und rechnen damit wesentlich länger. \(10\)-\(20\) Knoten reichen vollkommen.
Zwei Spezies
Lösen Sie ganz einfach zwei entkoppelte Diffusionsleichungen. Es geht nur darum, zu testen, ob die Implementation von zwei Spezies fehlerfrei funktioniert.
4.6.2 Teilchen driften unter dem Einfluss eines elektrischen Feldes
2 Punkte
Legen Sie einen Potenzialunterschied zwischen der linken und rechten Platte an und überprüfen Sie, dass sich geladene Teilchen in die richtige Richtung bewegen. Sie können eine Dirac-ähnliche Anfangskonzentration verwenden und zeigen Sie, wie sich diese verschiebt. Es kann sein, dass Sie die effektive Ladung ihrer Ionen erhöhen müssen, um diesen Effekt zu sehen.
4.6.3 Spezies mit gleicher Ladung stoßen sich ab
2 Punkte
Zeigen Sie, dass sich Spezies mit gleicher Ladung auch abstoßen. Nutzen Sie zwei Dirac-ähnliche Funktionen als Anfangsbedingungen und kein angelegtes elektrisches Feld.
4.6.4 Spezies mit Ladungen unterschiedlichen Vorzeichens ziehen sich an
1 Punkte
Zeigen Sie, dass zwei Spezies mit unterschiedlicher Ladung sich anziehen. Starten Sie mit zwei Spezies mit unterschiedlicher Ladung und keinem angelegten elektrischen Feld. Zwei versetzte Dirac-Peaks in der Konzentration sollten sich anziehen.
4.6.5 Validieren Sie Ihren Code quantitativ gegen eine bekannte analytische Lösung
2 Punkte
Für diesen (um \(x=0\)) symmetrischen Fall lässt sich die nichtlineare Poisson-Boltzmann-Gleichung über den Ansatz \begin {equation} \Phi (x) = \Phi _0 + \frac {k_B T}{ q_e} \ln {\cos ^2(K x)} \end {equation} lösen, wobei \(\Phi _0\) und \(K\) noch zu bestimmen sind. Für das Erfüllen der Differenzialgleichung muss \begin {equation} \Phi _0 = - \frac {k_B T}{q_e} \ln \Big ( \frac {2 k_B T \varepsilon }{q_e^2 c_{\infty }} K^2 \Big ) \end {equation} gelten. Erfüllen der Potential-Randbedingungung \(\Phi (L/2) = \Phi _1\) liefert eine transzendente Gleichung für \(K\), \begin {equation} \cos ^2 \Big (\frac {K L }{2}\Big ) - \exp \Big ( \frac {q_e}{k_B T} \Phi _1 \Big ) \frac {2 k_B T \varepsilon }{q_e^2 c_\infty } K^2 = 0, \end {equation} die numerisch gelöst werden muss. (Unten finden Sie eine Funktion, die scipy.optimize.root_scalar nutzt um diese Gleichung zu lösen.)
\(c_{\infty }\) ist die Konzentration des Bades mit elektrischem Potential \(\Phi = 0\), das im Gleichgewicht mit dem betrachteten Behälter steht. Da das elektrische Potential am linken und am rechten Rand in unserer Simulation auch gleich Null ist, muss dort die Gleichgewichtskonzentration gleich \(c_\infty \) sein. Messen Sie diese Konzentration und setzen Sie \(c_\infty \) auf diesen Wert.
Zeigen Sie, dass die numerische Lösung für große Zeitschritte mit der analytischen Lösung übereinstimmt.
2 """
3 Solution of the Poisson-Boltzmann equation for 1 species
4 between two plates with fixed potential.
5
6 The solution is connected with a bath with
7 potential 0 and concentration ‘concentration_bath‘.
8
9 Parameters
10 ----------
11 x : array_like
12 Position in units of the debye length
13 wall_distance : float
14 Wall distance in units of the debye length
15 potential_wall : float
16 Electric potential at the wall in units of the thermal voltage
17
18 Returns
19 -------
20 potential_g : numpy.ndarray
21 The potential evaluated at x in units of the thermal voltage
22 """
23 from scipy.optimize import root_scalar
24
25 # solve the transcendental equation for K
26 L = wall_distance
27 sol = root_scalar(
28 lambda K:
29 np.cos(K * L / 2) ** 2
30 - 4 * K ** 2 * np.exp(potential_wall),
31 x0=np.pi / L * 0.9999,
32 x1=np.pi / L * 0.0001,
33 )
34 assert sol.converged
35
36 _K = sol.root
37
38 return (- np.log(_K ** 2 * 4)
39 + np.log(np.cos(_K * (x)) ** 2))
4.7 Zyklische Anregung
Wir wollen uns jetzt der Modellierung eines Kondensators unter zyklischer Anwendung widmen. Modifizieren Sie Ihren Code so, dass Sie das Potential auf der rechten Seite des Kondensators zeitlich variieren können. Regen Sie Ihr System nun mit einer Dreiecksanregung an. Mit der Funktion scipy.signal.sawtooth können Sie direkt ein solchen Signal erzeugen. Das folgende Bild zeigt ein entsprechendes Anregungsprofil.
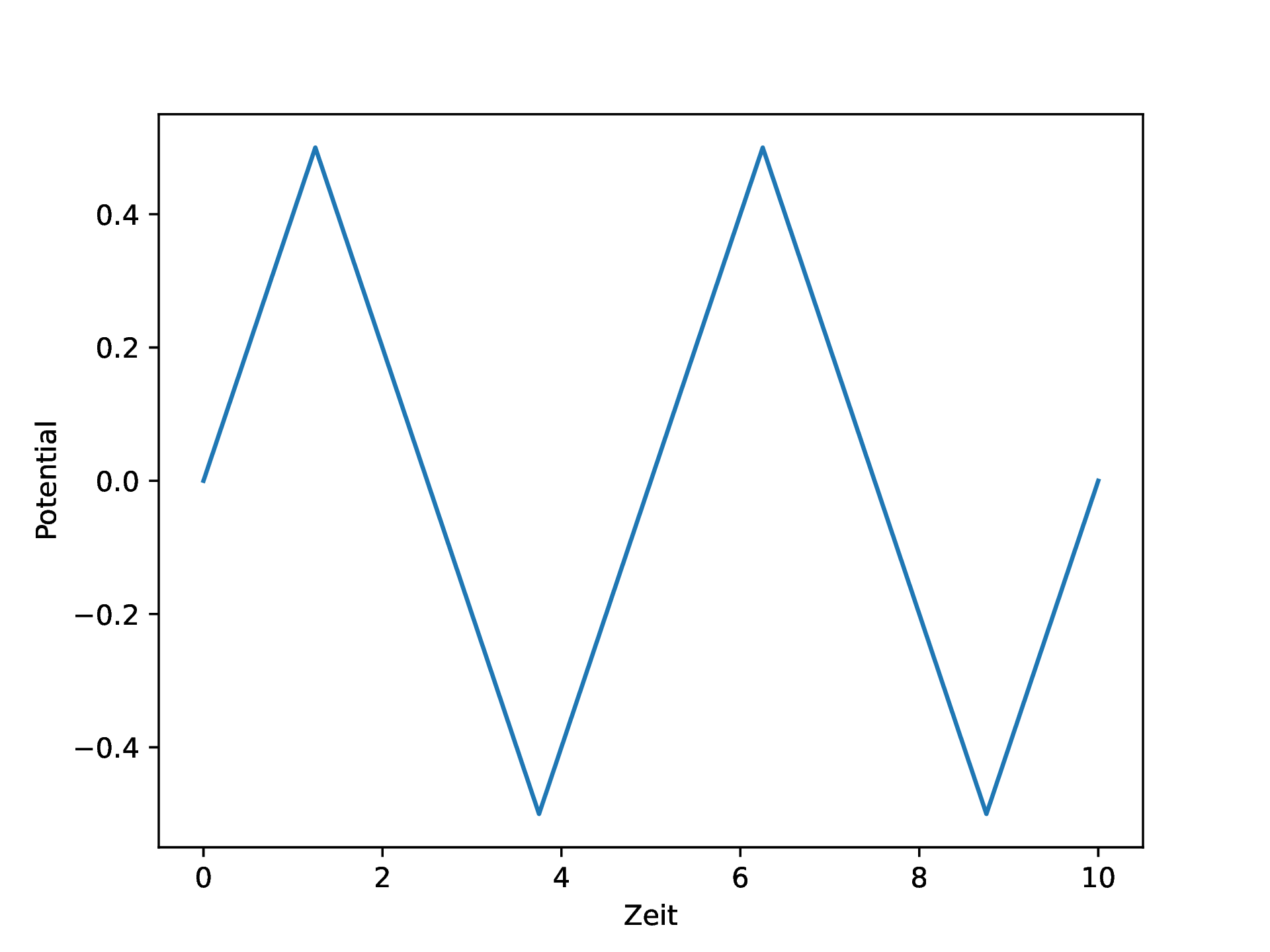
Zeigen Sie nun die Ionenkonzentration und den Potentialverlauf über den Kondensator als Funktion der Zeit. (Sie können hier auch gerne ein Video von machen!) Nutzen Sie hierfür zunächst eine Länge von \(L=1\) (also dem \(1\)-fachen der Debye-Länge) und eine Periode von \(T=1\). Die Anfangkonzentration darf konstant sein und \(1\) betragen. Die Amplitude der Anregung sollte auch \(1\) sein. Achten Sie darauf, dass zum Anfang der Simulation das Potential auf beiden Elektroden identisch ist.
Zeigen Sie die Fälle:
- \(L=1\), \(T=1\)
- \(L=10\), \(T=1\)
- \(L=10\), \(T=10\)
- \(L=10\), \(T=100\)
Wie unterscheiden sich diese Fälle und warum? Interessant sind insbesondere die Ionenkonzentrationen und Potentialverläufe bei den maximalen und minmialen Spannungen (Potentialdifferenzen).
Anmerkung:
- Sie müssen die Referenzlänge \(1\), also die Debye-Länge, mit ein paar Gitterpunkten diskretisieren. Dies ist nötig weil typische Konzentrationsabfälle über diese Länge stattfinden und Sie diese noch erfassen müssen.
- Die Rechnungen mit \(T=100\) werden vermutlich länger rechnen.
4.8 Cyclovoltammogramm
5 Punkte
Wir wollen uns nun in dieser letzten Aufgabe der Berechnung eines Cyclovoltammogramms (CVs) widmen. Hierzu wird der Ladung als Funktion der Spannung geplottet. Wie lautet der Ausdruck für die Ladung auf den Kondensatorplatten? Implementieren Sie diesen in eine Hilfsfunktion.
Anmerkung: Ein CV ist eigentlich Strom als Funktion der Spannung, wir schauen uns hier aber die Ladung an. Sie können den Strom natürlich als zeitliche Veränderung der Ladung, also als Ableitung eines Ladungs-Spannungs-Diagramms, bestimmen.
Implementieren Sie nun eine Funktion, die Ihnen ein Cyclovoltammogramm für Ihren Kondensator ausrechnet.
Berechnen Sie die CVs für die oben genannten Parameter. Es macht Sinn die CVs über 5 Perioden aufzunehmen. Was sehen Sie und warum?
4.9 Dünnbesetzte Algorithmik
0 Punkte
Schreiben Sie Ihre Funktion so um, dass sie dünnbesetzte Arithmetik aus dem Paket scipy.sparse nutzt. Dies reduziert die Komplexität der Lösung eines linearen Gleichungssystem von \(\mathcal {O}(N^2)\) auf \(\mathcal {O}(N)\). D.h. wenn Sie Ihre Gitterpunkte verdoppeln, sollte der Code dann nur doppelt (und nicht viermal) so langsam laufen.
Anmerkung: Nutzen Sie das “compressed sparse row (CSR)” Format scipy.sparse.csr_matrix. Für die Lösung linearer Gleichungssysteme müssen Sie dann scipy.sparse.linalg.spsolve nutzen.