Kapitel 1
Einleitung
Kontext: Die Simulation beschäftigt sich mit der numerischen (computergestützten) Lösung von Modellen. In diesem einleitenden Kapitel gehen wir auf Modellbildung ein und stellen unterschiedliche Klassen von Modellen vor. Diese Modelle werden mathematisch üblicherweise mit Hilfe von Differentialgleichungen beschrieben, d.h. die Simulation ist oft (aber nicht immer) die numerische Lösung von gewöhnlichen oder partiellen Differentialgleichungen. In dieser Lehrveranstaltung werden wir vornehmlich die Lösung von partiellen Differentialgleichungen mit Hilfe der Methode der finiten Elemente besprechen.
1.1 Modelle
Modelle sind üblicherweise für bestimmte Längenskalen angemessen. So kann z.B. ein Modell, welches explizit Atome beschreibt, auf Längenskalen \(\sim \text {nm}\) angemessen sein; ein “makroskopisches” System mit Abmessungen \(\sim \text {mm}\) würden wir mit einem solchen Modell aber nicht beschreiben wollen. Wir müssen uns daher darüber klar werden, welches der Phänomene der Ingenieurswissenschaften die Anwendung welcher physikalischer Modelle und welcher mathematischer Methoden verlangt.
Anmerkung: “Wollen” ist hier das falsche Wort. Zum einen ist es auf Grund begrenzter Computerressourcen nicht möglich, zum anderen versteckt sich in einem solchen Modell unter Umständen die essentielle Frage, die wir beantworten wollen, wie die legendäre Nadel im Heuhaufen.
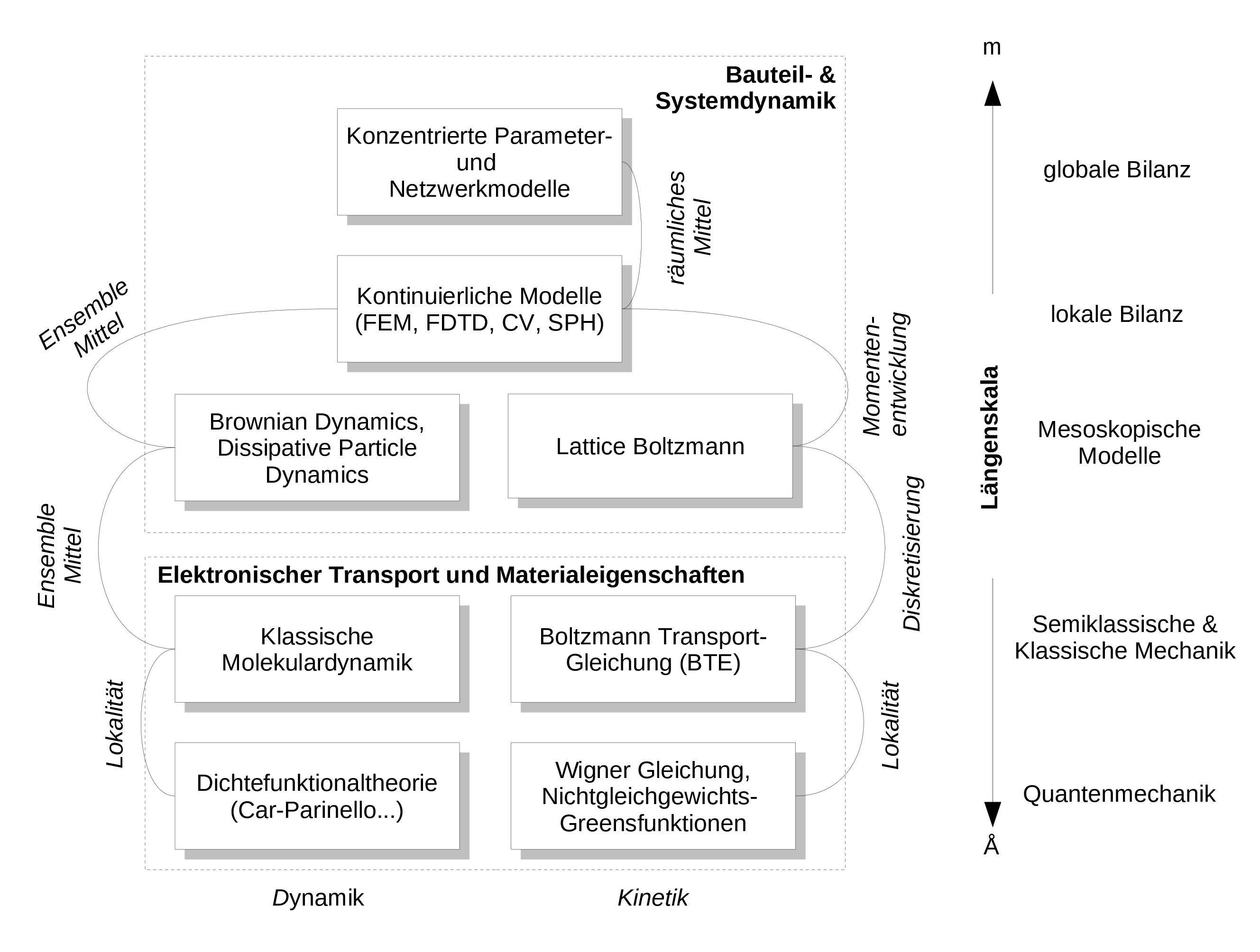
Abbildung 1.1 zeigt in der vertikalen Anordnung von Längenskalen und deren Zuordnung zu verschiedenen Beschreibungsebenen. Auf der kürzesten Längenskala ist meist eine quantenmechanische Beschreibung notwendig. Dies bedeutet, wenn wir die Phänomene in Å auflösen wollen, befinden wir uns auf der Beschreibungsebene der Quantenmechanik und alle zugrundeliegenden Modelle sind von quantenmechanischer Natur. D.h. wir haben es hier im nichtrelativistischen Fall mit der Schrödingergleichung zu tun. Diese ist in verschiedenen Methoden implementiert, wie z.B. der Dichtefunktionaltheorie, einer Vielteilchenbeschreibung des quantenmechanischen elektronischen Systems. Bei dieser Art der Vielteilchenbeschreibung handelt es sich, im Gegensatz zur Molekulardynamik als Methode auf einer größeren Längenskala, nicht um eine Beschreibung von Punktteilchen, sondern um gekoppelte Felder, was den Aufwand im Vergleich zu einer reinen Punktmechanik wesentlich erhöht. In der Punktmechanik haben wir es mit drei Orts- und drei Geschwindigkeitsvariablen für jedes der \(n\) wechselwirkenden Teilchen zu tun, während wir in einer quantenmechanischen Vielteilchenbeschreibung es mit einem Feld mit je drei \(n\) Ortsvariablen zu tun haben, nämlich \(\Psi (\v {r}_1,\v {r}_2,\dots ,\v {r}_n;t)\).
Anmerkung:
- \(1\,\AA =10^{-10}\,\text {m}\)
- Atome in unserer Umwelt werden durch quantenmechanische Phänomene zusammengehalten. Modelle die auf quantenmechanischen Prinzipien fußen, heißen auch ab-initio (“von Anfang an”) Modelle. Im Englischen werden solche Modell auch als “first principles” Modelle bezeichnet. Die fundamentale Gleichung, welche quantenmechanische Objekte beschreibt, ist die Schrödingergleichung. Diese selbst ist in der Tat bereits eine Näherung!
- Die Einteilchen-Schrödingergleichung lautet \(i\hbar \frac {\partial }{\partial t} \Psi (\v {r},t) = \hat {H} \Psi (\v {r},t)\). Dies ist eine partielle Differentialgleichung für das orts- und zeitabhängige skalare Materiefeld \(\Psi (\v {r},t)\), mit der Planckschen Konstanten \(\hbar \) und dem Hamiltonoperator \(\hat {H}\), der die Details des Modells enthält. Eine Bewegungsgleichung für viele wechselwirkende Teilchen, wie sie durch \(\Psi (\v {r}_1,\v {r}_2,\dots ,\v {r}_n;t)\) beschrieben wird, ist unvergleichlich umfangreicher.
- “Semiklassisch“ bedeutet, dass die Bewegung der Teilchen nach der klassischen Mechanik berechnet werden, die Wechselwirkungen der Teilchen untereinander aber aus quantenmechanischen Gesetzen abgeleitet sind. Dies ist natürlich eine Näherung, die es zu rechtfertigen gilt.
- “Mesoskopisch” heißt, dass das Modell über eine innere Längenskala verfügt und/oder thermische Fluktuationen wichtig sind. Diese Modelle operieren meistens auf Längenskalen oberhalb der atomaren Skala (\(\sim \) nm) aber unterhalb der Skalen unserer Wahrnehmung der Umwelt (\(\sim \) mm).
- “Bilanz” heißt, dass der Kern der Beschreibung eine Erhaltungsgröße ist, die einfach gezählt werden kann. Erhalten sind z.B. Teilchenzahlen. Eine Bilanzgleichung oder Bilanzierung zählt dann einfach die Teilchen, die über ein gewisses Zeitinterval in ein Volumen hinein fließen, heraus fließen oder darin produziert werden. Weitere Erhaltungsgrößen, die man bilanzieren kann, sind der Impuls und die Energie. Die Bilanzgleichung wird auch Kontinuitätsgleichung genannt.
Auf der Ebene der semiklassischen und klassischen Mechanik, auch als kinetische Ebene bezeichnet, werden die Modelle entweder durch die Molekulardynamik beschrieben oder durch die Bewegungsgleichung der Einteilchen-Wahrscheinlichkeitsdichte im Phasenraum \(f(\v {r},\v {p})\) - mit den unabhängigen Variablen Ort \(\v {r}\) und Impuls \(\v {p}\). Im zweiten Fall haben wir eine Funktion \(f(\v {r}(t),\v {p}(t),t)\) die von Ort, Impuls und der Zeit sowohl explizit, als auch implizit über \(\v {r}(t)\) und \(\v {p}(t)\) abhängt. Nehmen wir an, wir müssen \(f(\v {r}(t),\v {p}(t),t)\) durch diskrete Stützstellen interpolieren. Dies sind bei einer geringen Auflösung von 10 Punkten pro Variabler schon bereits 10.000.000 Interpolationspunkte. Dies ist vielleicht handhabbar, die Auflösung ist aber nicht besonders gut. Und daher ist dieses Unterfangen eher unnütz. Wir wollen nicht verschweigen, dass es durchaus Methoden zur numerischen Lösung der beiden oben beschriebenen Probleme gibt, auf diese werden aber in dieser Veranstaltung nicht näher eingegangen.
1.2 Partikel
Grob können wir daher zwei Arten von Modellen unterscheiden: Modelle, die einzelne diskrete Elemente, beispielsweise Partikel (Atome, Moleküle, Körner, etc.), als zentrales Element haben und Modelle die kontinuierliche Felder (elektrostatisches Potential, Ionenkonzentrationen, mechanische Spannungen und Dehnungen) als zentrales Element haben. Im ersten Modelltyp werden Evolutionsgleichungen für diskrete Eigenschaften, welche auf den Partikeln definiert sind, wie z.B. deren Positionen \(\v {r}_i\) und Geschwindigkeiten \(\v {v}_i\), formuliert.
Um beispielsweise die Kinetik dieser Partikel zu beschreiben, könnten wir die Newtonschen Bewegungsgleichungen lösen. D.h. wir müssen für jedes der \(n\) Teilchen \(6\) gewöhnliche Differentialgleichungen, die noch untereinander gekoppelt sind, lösen, nämlich: \begin {equation} \dot {\v {r}}_i(t)=\v {v}_i(t)=\frac {\v {p}_i(t)}{m_i} \label {eq:posupdate} \end {equation} Dies ist die Gleichung für die Bahnkurve des Teilchens \(i\) im Ortsraum. Da \(\v {r}\) ein Vektor ist, ist Gl. \eqref{eq:posupdate} ein System aus \(3\) gewöhnlichen Differentialgleichungen. Die Geschwindigkeit \(\v {v}_i\) des Teilchen \(i\) zum Zeitpunkt \(t\) unterliegt durch den Impuls \(\v {p}_i\) ebenfalls einem System von Differentialgleichungen: \begin {equation} \dot {\v {p}}_i(t)=\sum _j\v {F}_{ij}(t) \label {eq:velupdate} \end {equation} Gleichung \eqref{eq:velupdate} beschreibt die zeitliche Entwicklung des Impulses des Teilchens \(i\). Gleichung \eqref{eq:posupdate} und \eqref{eq:velupdate} sind je \(3\times n\) gekoppelte gewöhnliche Differentialgleichungen. Wollen wir z.B. die Bewegung sämtlicher Moleküle in einem Liter Wasser durch eine Simulation beschreiben, so ist dies ob der großen Zahl an Gleichungen unmöglich und wir müssen übergehen zu einer Beschreibung mit Hilfe von Bilanzgleichungen und Feldern.
Die Newtonschen Bewegungsgleichungen \eqref{eq:posupdate} und \eqref{eq:velupdate} sind von ihrer Natur her physikalische Grundprinzipien. Sie gelten so für Atome oder Planeten. Die Natur der Kraft selbst, \(\v {F}_{ij}\) in den Gleichungen oben, basiert natürlich auf physikalisch beschreibbaren Effekten, ist aber nicht notwendigerweise ein Naturprinzip. Als einfaches Beispiel sei die Lennard-Jones-Wechselwirkung genannt, für welche die Wechselwirkungsenergie \begin {equation} V_{ij} = 4\varepsilon \left [ \left (\frac {\sigma }{r_{ij}}\right )^{12} - \left (\frac {\sigma }{r_{ij}}\right )^{6}\right ] \label {eq:lj_potential} \end {equation} und damit die Kraft \begin {equation} \v {F}_{ij} = -4\varepsilon \left [ 12\left (\frac {\sigma ^{12}}{r_{ij}^{13}}\right ) - 6\left (\frac {\sigma ^{6}}{r_{ij}^{7}}\right )\right ]\hat {r}_{ij} \label {eq:lj} \end {equation} gilt, wobei \(r_{ij}\) der Abstand zwischen den Partikeln (hier Atomen oder Molekülen) \(i\) und \(j\) ist. Der Term \(\propto r^{-13}\) beschreibt die Abstoßung der Atome auf Grund des Paulischen Ausschließungsprinzips und der Term \(\propto r^{-7}\) beschreibt die Anziehung der Atome auf Grund der Londonschen Dispersionswechselwirkung. Beide Wechselwirkungen fußen auf physikalischen Grundprinzipien, aber die Formulierung Gl. \eqref{eq:lj} reduziert diese komplexen Phänomene auf ein einfaches konstituierendes Gesetz. Solche Gesetze werden oft Konstitutivgesetze genannt. Die numerische Lösung der Newtonschen Bewegungsgleichungen für Atome wird als Molekulardynamiksimulation bezeichnet.
Anmerkung: Der Begriff Konstitutivgesetz taucht öfter im Rahmen von Feldtheorien auf. Für das Lennard-Jones-Potential ist dieser Begriff eher ungewöhnlich, dieses Gesetzes ist aber trotzdem durchaus einer konstitutiven Natur.
Ein weiteres Beispiel von Modellen mit diskreten Elemente sind Netzwerkmodelle für elektrische Schaltkreise. Hierbei verknüpft ein Element eine Potentialdifferenz (Energiedifferenz) mit einem fließenden Strom, beispielweise beschreibt \begin {equation} i = u / R \label {eq:resistor} \end {equation} den Strom \(i\), der durch einen Widerstand \(R\) fließt, über den die Spannung \(u\) abfällt. Hinzu kommen die Kirchhoffschen Regeln für Strom und Spannung. Solche Modelle werden im englischen oft als “lumped-element models” bezeichnet. Gleichung \eqref{eq:resistor} hat natürlich auch die Qualität eines Konstitutivgesetzes, da komplexe elektronische Prozesse hinter dem einzelnen Parameter \(R\) stehen. Die Kirchhoffschen Regeln hingegen haben die Qualität einer Bilanzgleichung. In Abb. 1.1 werden diese Modelle daher mit dem Begriff globale Bilanz bezeichnet. “Lumped-element models” führen auch zu Systemen gewöhnlicher Differentialgleichungen, die oft numerisch durch explizite Zeitpropagation gelöst werden. Bekannte Vertreter dieser Gattung Simulationssoftware sind z.B. SPICE oder MATLAB Simulink.
Diese globale Bilanzebene ist geprägt durch das Desinteresse an lokaler Auflösung. Wir interessieren uns nicht für Dichten, sondern nur für Gesamtmassen, nicht für Stromdichten sondern nur für Ströme. Am besten lässt sich dies an dem o.g. Widerstand verdeutlichen, dessen Kontakte auf unterschiedlichen Potentialen liegen. Dies hat im einfachsten Fall einen Stromfluss zur Folge. Wir fragen uns nicht, wie der Strom in dem Widerstand verteilt ist. Wir fragen nicht einmal, ob der Widerstand homogen oder inhomogen ist, wir nehmen ihn als Gesamtwert, als schwarzen Kasten, dem wir einen Parameterwert zuordnen. Diese Herangehensweise wurden schon ausführlich in der Elektrotechnik und der Systemtheorie besprochen.
1.3 Felder
Wenn wir nun aber feststellen, dass der schwarze Kasten mit einem Parameter nur ungenügend beschrieben ist, dann fangen wir an, ihn zu ersetzen durch einen komplexeren Ersatzschaltkreis mit Details, die den inneren Zustand des Bauteils auflösen. Dies kann man wiederum soweit treiben, dass zum Schluss ein Kontinuum entsteht - wir sind auf der lokalen Bilanzebene angekommen. Dazu wiederum brauchen wir Parameter, wie z.B. die Leitfähigkeit, die Viskosität oder die Diffusivität, die ihrerseits als Modelle nicht aus der kontinuierlichen Beschreibung der lokalen Bilanz ableitbar sind. Man braucht beispielsweise Experimente oder ab-initio Simulationen, um diese Größen zu ermitteln.
Lokale Bilanz bedeutet, dass wir an jedem Raumpunkt dem System eine Dichte, Konzentration, Temperatur oder ähnliche Größe zuordnen können. Damit sind aber die zeitlichen Veränderungen der Ortsfreiheitsgrade - also die Impulse, respektive die Geschwindigkeiten - in ihrer Verteilung durch eine lokale, thermodynamische Gleichgewichtsbedingung festgelegt. (Die Impulse genügen im thermodynamischen Gleichgewicht einer Maxwell-Boltzmann Verteilung.) Dieses lokale Gleichgewicht bedeutet nicht, dass wir keine Dynamik mehr haben. Aber wenn wir an einen Schwarm von Gas- oder Flüssigkeitsteilchen denken, dann folgen eben deren individuelle Geschwindkeiten einer Gleichgewichtsverteilungsfunktion, deren Mittel folgt aber der Bilanzgleichung. Die Dynamik läuft also gemittelt über eine riesige Zahl dieser Teilchen hinweg ab. Lokale Bilanz bedeutet auch nicht, dass an unterschiedlichen Orten nicht unterschiedliche Temperaturen oder Dichten vorliegen können. Die Unterschiede in diesen Parametern sind dann die treibenden Kräfte der Dynamik - Temparaturgradient, Dichtegradient, etc.
Solche Modelle fallen in den Bereich der Feldtheorien, und deren mathematische Beschreibung erfolgt über partielle Differentialgleichungen. (Dies steht im Gegensatz zu den gewöhnlichen Differentialgleichungen der diskreten Modelle.) Eine Feldtheorie, die auf Bilanzierung von Masse, Impuls oder Energie basiert, benötigt immer Konstitutivgesetze für die Beschreibung des Materialverhaltens. Diese Konstitutivgesetze enthalten Transportparameter wie die Viskosität oder Diffusionskonstante. Es gibt auch Feldtheorien, die den Charakter eines physikalischen Grundprinzips haben. Dies ist beispielsweise die o.g. Schrödingergleichung oder aber auch die Maxwell-Gleichungen der Elektrodynamik. In dieser Lehrveranstaltung wollen wir uns auf solche kontinuierliche Systeme konzentrieren, die als Feldtheorie mit Hilfe von partiellen Differentialgleichungen formuliert werden.
1.4 Welches Modell ist das richtige?
Wohlgemerkt, wir haben keine der Beschreibungsebenen auf verschiedenen Längenskalen mit irgendeiner Wertung versehen. Nur weil sie Quantenmechanik heisst und den Einen oder die Andere ob ihrer Komplexität in Ehrfurcht erstarren lässt, bietet sie nicht notwendigerweise die Lösung. Ganz im Gegenteil, es kann sogar hinderlich sein, zu viel Detail aufösen zu wollen und wir müssen uns ständig fragen, wieviel Detail in der Simulation notwendig ist. Mehr noch, fragen wir uns stets bevor wir eine Simulation angehen: “Ist eine Simulation dieser Komplexität wirklich notwendig, oder kann ich das Problem vereinfachen?” Die Simulation sollte als Hilfsmittel gesehen werden und nicht als Selbstzweck, frei nach dem amerikanischen Mathematiker Richard Wesley Hamming (*1915, \(\dagger \)1998): The purpose of computing is insight, not numbers.