Kapitel 11
Datenstrukturen & Implementierung
Kontext: In diesem Kapitel wird Anhand unseres Beispiels, der Lösung der Poisson-Gleichung, gezeigt, wie nun ein einfacher Finite-Elemente-Löser in der Programmiersprache Python implementiert werden kann. Wir nehmen hier an, dass die Ladungsdichte verschwindet. Wir berechnen also die räumliche Verteilung des elektrostatischen Potentials unter entsprechenden Randbedingungen. Dies werden wir nutzen, um die Kapazität eines Plattenkondensators auszurechnen.
11.1 Beispielproblem
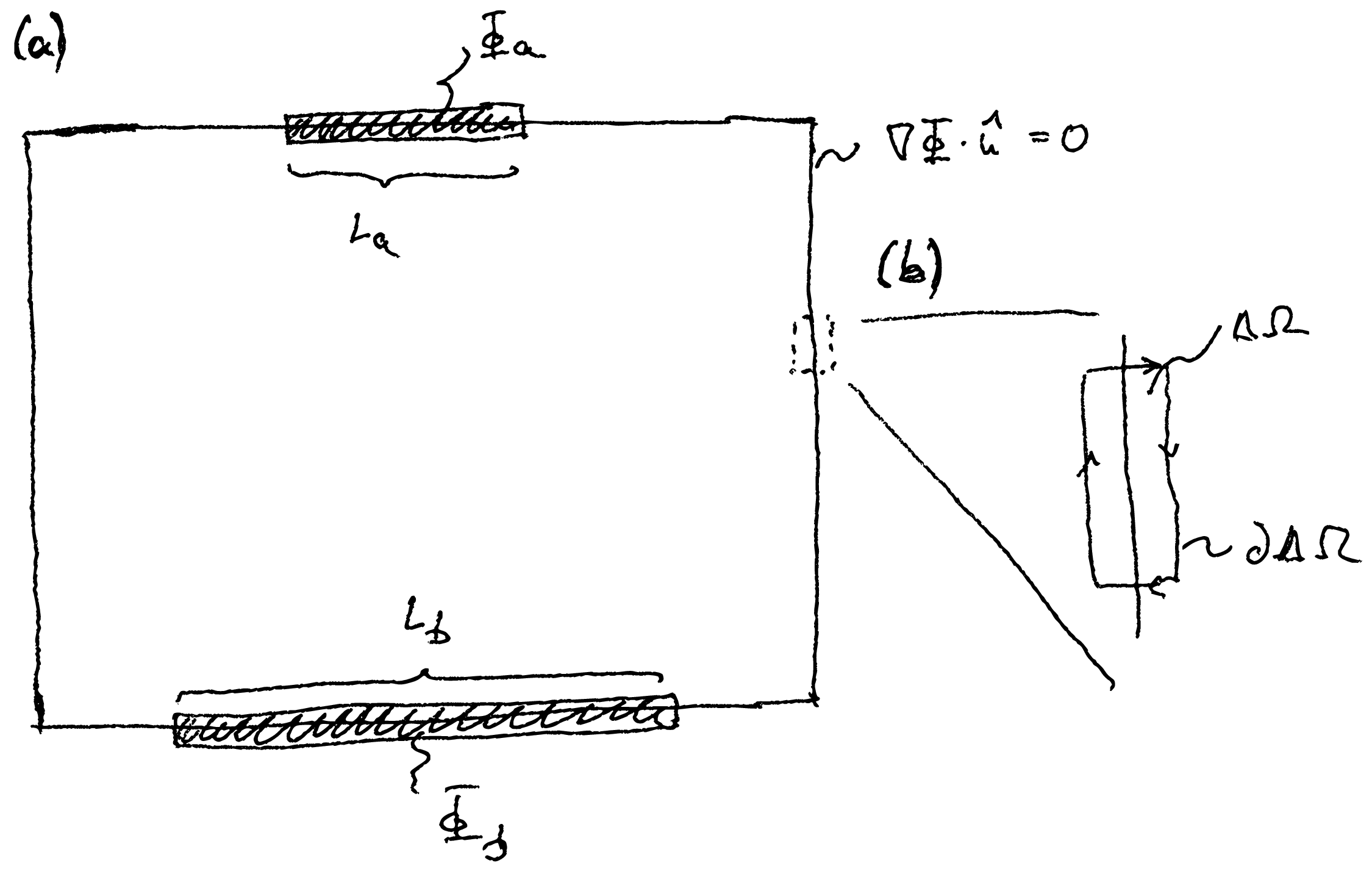
Wir werden nun unser Beispielproblem aus den vorhergehenden Kapitel weiterentwickeln und die Kapazität eines Plattenkondensators berechnen. Hierfür nehmen wir eine verschwindende Ladungsdichte im Kondensator an, \(\rho =0\). Die Poisson-Gleichung wird dann zur Laplace-Gleichung, \begin {equation} \nabla ^2 \Phi = 0. \end {equation} Die Platten des Kondensators werden als metallisch angenommen, d.h. das Potential auf den Kondensatorplatten ist konstant (siehe Abb. 11.1a). Dies wird durch eine Dirichlet-Randbedingung abgebildet. Der Rest des Gebiets erhält eine Neumann-Randbedingung, in der die Ableitung auf der Oberfläche verschwindet.
Im Kontext der Poisson- bzw. Laplace-Gleichung haben Richtungsableitungen am Rand eine einfache Interpretation. Wir schauen uns ein kleines Volumenelement \(\Delta \Omega \) am Rand des Gebiets an (siehe Abb. 11.1b). Integration der Poisson-Gleichung über dieses Gebiet ergibt, \begin {equation} \int _{\Delta \Omega }\dif ^3 r\, \nabla ^2 \Phi = \int _{\partial \Delta \Omega }\dif ^2 r\, \nabla \Phi \cdot \hat {n}(\v {r}) = \frac {1}{\varepsilon } \int _{\Delta \Omega }\dif ^3 r\, \rho (\v {r}), \end {equation} wobei die Integration über \(\partial \Delta \Omega \) entlang des in Abb. 11.1b gezeigten Pfades erfolgt. Nun nehmen wir an, dass die beiden Seiten des Pfades, die senkrecht auf den Rand des Gebiets stehen, vernachlässigbar gegenüber den beiden anderen Seiten sind. Weiterhin nehmen wir an, dass in dem Gebiet lediglich eine Oberflächenladung \(\sigma (\v {r})\) lebt. Damit erhält man \begin {equation} \int _{\partial \Delta \Omega }\dif ^2 r\, \nabla \Phi \cdot \hat {n}(\v {r}) = \frac {1}{\varepsilon } \int _{\Delta A}\dif ^2 r\, \sigma (\v {r}), \end {equation} wobei \(\Delta A\) die Fläche des Randes des Simulationsgebiets ist, welcher in \(\Delta \Omega \) liegt. Nimmt man nun an, dass der Raum außerhalb des Simulationsgebietes feldfrei ist, also \(\nabla \Phi =0\), dann erhält man \begin {equation} \nabla \Phi \cdot \hat {n}(\v {r}) = \frac {\sigma (\v {r})}{\varepsilon }, \label {eq:surfacecharge} \end {equation} die Richtungsableitung ergibt also die Oberflächenladung am Rand.
Die Feldfreiheit außerhalb unserer Simulationsdomäne ist exakt nur an den Elektroden erfüllt. Diese sind metallisch und daher per Definition feldfrei. (Ein Feld innerhalb eines idealen Metalls führt sofort zu einer Umordnung von Ladungen, die dieses Feld dann kompensieren.) D.h. wir können Gl. \eqref{eq:surfacecharge} nutzen, um die auf den Kondensatorplatten induzierte Ladung zu berechnen. Zusammen mit dem durch die Dirichlet-Randbedingungen vorgegebenen Potential, kann dies zur Berechnung der Kapazität auf den Kondensatorplatten genutzt werden.
Auf der anderen Seite heißt die implizite Neumann-Randbedingung \(\nabla \Phi \cdot \hat {n}=0\), dass unsere Simulation unter Bedingungen durchgeführt wird, in denen der Rand ladungsfrei ist aber außerhalb der Simulationsdomäne das Feld verschwindet. Dies ist eine künstliche Bedingung, die Fehler verursachen kann. Man muss also sicherstellen, dass die Simulationsdomäne in Richtung parallel zu den Kondensatorplatten groß genug ist, um die Streufelder am Rand den Kondensators vernünftig zu erfassen.
11.2 Datenstrukturen
Die zentrale Datenstruktur für numerische Anwendungen ist der multidimensionale Array, numpy.ndarray, der numpy-Bibliothek. Multidimensionale Arrays halten Speicher für eine gewisse Menge an Einträgen vor. (Diese Einträge werden auch Elemente genannt, aber um diese nicht mit den finite Elementen durcheinander zu werden, werden sie in diesem Dokument durchgehend Einträge genannt.) Ein mit Nullen gefülltes Array der Länge \(10\) (also \(10\) Einträge) erhält man durch
Diese Array hat die Dimension \(1\). Der mehrdimensionale Charakter der Arrays äußert sich darin, dass die Arrays implizit eine Abbildung von mehreren Koordinaten auf einen lineare Index implementieren. Einen zweidimensionalen Array bekommt man z.B. durch
Man kann nun jeweils auf die Array-Einträge zugreifen, z.B.
Beide Befehle greifen auf Eintrag \(6\) des zu Grunde liegenden Speicherbereichs zu. Ein natürlicher Einsatz der multidimensionalen Arrays ist die Repräsentation von Vektoren (\(1\)-dimensionale Arrays) oder Martrizen (\(2\)-dimensionale Arrays).
Anmerkung: Die Aussage, dass
in dem o.g. Beispiel auf den gleichen Eintrag des zu Grunde liegenden Speicherbereichs zugreift, hängt von der Speicherreihenfolge (engl. “storage order”) ab. Sie gilt nur dann, wenn der letzte Index kompakt im Speicher steht. Diese Speicherreihenfolge nennt sich “row major”, weil in einem zweidimensionalen Array, also einer Matrix, die Zeilen (engl. “row”) kompakt im Speicher stehen. Ist der erste Index der kompakte spricht man von “column major”. In numpy heißt “row major” auch “C-continguous” und “column major” heißt “F-contiguous”. Dies kommt daher, dass in der Programmiersprache C die Speicherreihenfolge “row major” und in der Programmiersprache Fortran die Speicherreihenfolge “column major” ist. Arrays in numpy sind standardmäßig “column major”, andere Speicherreihenfolgen werden aber unterstützt und kommen auch vor.
11.3 Initialisierung
Die Beispielimplementierungen folgen einfache Regeln für lesbaren Computercode. Dieser sollte immer so geschrieben sein, dass eine dritte Person diesen lesen und wiederverwenden kann. Wir werden daher...
- ...ausschließlich englische Sprache verwenden.
- ...Variablennamen ausschreiben und keine Symbole als Variablennamen verwenden (also z.B. potential und nicht das ausgeschriebene Symbol phi als Name).
- ...Array-Variablen mit einem Suffix versehen, der den Typ der Indices anzeigt (z.B. potential_xy um anzuzeigen, dass es zwei Indices gibt die den Positionen \(x\) und \(y\) entsprechen).
- ...den Code mit Kommentarblöcken und Python Docstrings dokumentieren. Wir empfehlen den numpydoc-Standard für Docstrings.
In dieser Implementierung verwenden wir explizite Schleifen, um die Lesbarkeit des Codes zu verbessern. Der Code kann durch Verwenden von numpy-Operationen noch vektorisiert werden.
Zunächst müssen wir den Code initialisieren und festlegen, wieviele Gitterpunkte wir verwenden wollen. Wir definieren die Variablen
Wir legen nun auch noch fest, über welchen Bereich sich die beiden Elektroden des Kondensators erstrecken sollen:
2top_left = Nx//4
3top_right = 3*Nx//4-1
4top_potential = 1
5
6# Bottom capacitor plate
7bottom_left = Nx//4
8bottom_right = 3*Nx//4-1
9bottom_potential = -1
Der Bereich wird hier mit Knotenindices angegeben. Weiterhin benötigen wir noch die Elementmatrix die wir in einem numpy.ndarray speichern:
2element_matrix_ll = np.array([[1, -1/2, -1/2],
3 [-1/2, 1/2, 0],
4 [-1/2, 0, 1/2]])
Der Suffix _ll bezeichnet hier, dass es zwei Indices gibt (der Array ist zweidimensional), die beide einen lokalen Elementknoten bezeichnen. Wir initialisieren weiterhin die Systemmatrix und die rechte Seite, zunächst mit Nullen:
2system_matrix_gg = np.zeros([Nx*Ny, Nx*Ny])
3
4# Right hand side
5rhs_g = np.zeros(Nx*Ny)
Der Suffix _g bezeichnet hier den Index des globalen Knoten. Die Variable rhs_g enthält den Vektor \(\v {f}\) und benötigt daher nur einen Index. Die Variable system_matrix_gg beinhaltet die Systemmatrix \(\t {K}\) und braucht daher zwei globale Knotenindices.
11.4 Systemmatrix
Kern des Simulationsprogramms ist der Aufbau der Systemmatrix. In diesem Abschnitt wird dies durch explizite Schleifen realisiert. Im nächsten Abschnitt wird gezeigt, wie dies mit speziellen numpy-Befehlen kompakter (und effizienter), aber weniger transparent gestaltet werden kann.
Zunächst definieren wir eine Funktion, die aus Knotenkoordinaten den globalen Knotenindex macht:
2 """
3 Turn node coordinates (i, j) into their global node index.
4
5 Parameters
6 ----------
7 i : int
8 x-coordinate (integer) of the node
9 j : int
10 y-coordinate (integer) of the node
11 nb_nodes : tuple of ints
12 Number of nodes in the Cartesian directions
13
14 Returns
15 -------
16 g : int
17 Global node index
18 """
19 Nx, Ny = nb_nodes
20 return i + Nx*j
Dies nutzen wir in einer weiteren Hilfsfunktion, die die Elementmatrix zu der Systemmatrix addiert. Hierzu muss zunächst die Elementmatrix auf die Systemmatrix aufgespannt werden. Die Funktion sieht folgendermaßen aus:
2 global_node_indices):
3 """
4 Add element matrix to global system matrix.
5
6 Parameters
7 ----------
8 system_matrix_gg : array_like
9 N x N system matrix where N is the number of global
10 nodes. This matrix will be modified by this function.
11 element_matrix_ll : array_like
12 n x n element matrix where n is the number of local
13 nodes
14 global_node_indices : list of int
15 List of length n that contains the global node
16 indices for the local node index that corresponds to
17 the list position.
18 """
19 assert element_matrix_ll.shape == \
20 (len(global_node_indices), len(global_node_indices))
21 for i in range(len(global_node_indices)):
22 for j in range(len(global_node_indices)):
23 system_matrix_gg[global_node_indices[i],
24 global_node_indices[j]] += \
25 element_matrix_ll[i, j]
Die assert-Anweisung ist hier ein Wächter, der darauf achtet, dass die lokale Elementmatrix und der Array global_node_indices die gleiche Länge haben. Die beiden for-Schleifen laufen dann über alle Einträge der Elementmatrix. Der Ausdruck global_node_indices[i] liefert dann den globalen Knotenindex, der zu dem lokalen Knotenindex der Elementmatrix gehört. Der Zusammenbau der Systemmatrix erfolgt dann über einen Aufruf dieser Hilfsmethode pro Element:
2 """
3 Assemble system matrix from the element matrix
4
5 Parameters
6 ----------
7 element_matrix_ll : array_like
8 3 x 3 element matrix
9 nb_nodes : tuple of ints
10 Number of nodes in the Cartesian directions
11
12 Returns
13 -------
14 system_matrix_gg : numpy.ndarray
15 System matrix
16 """
17
18 Nx, Ny = nb_nodes
19 Mx, My = Nx-1, Ny-1 # number of boxes
20
21 # System matrix
22 system_matrix_gg = np.zeros([Nx*Ny, Nx*Ny])
23
24 # Construct system matrix
25 for l in range(Mx):
26 for m in range(My):
27 # Element (0)
28 n0 = node_index(l, m, nb_nodes)
29 n1 = node_index(l+1, m, nb_nodes)
30 n2 = node_index(l, m+1, nb_nodes)
31 add_element_matrix(system_matrix_gg,
32 element_matrix_ll,
33 [n0, n1, n2])
34
35 # Element (1)
36 n0 = node_index(l+1, m+1, nb_nodes)
37 n1 = node_index(l, m+1, nb_nodes)
38 n2 = node_index(l+1, m, nb_nodes)
39 add_element_matrix(system_matrix_gg,
40 element_matrix_ll,
41 [n0, n1, n2])
42
43 return system_matrix_gg
Hier laufen die beiden for-Schleifen über die einzelnen Kästen. Die Schleife über die beiden Elemente pro Kasten ist explizit als zwei Aufrufe zu add_element_matrix geschrieben. Die Variablen n0, n1 und n2 enthalten die globalen Knotenindices, die die Ecken des jeweiligen Elements beschreiben.
Die nun aufgebaute Systemmatrix hat (implizit) Neumann-Randbedingungen mit \(\nabla \Phi \cdot \hat {n}(\v {r})=0\) auf dem Rand. Wir müssen nun noch die Dirichlet-Bedingungen für die Elektroden hinzufügen. Hierzu ersetzen wir Zeilen der Systemmatrix und die entsprechenden Einträge des Lastvektors:
2 top_left, top_right, top_potential,
3 bottom_left, bottom_right, bottom_potential,
4 nb_nodes):
5 """
6 Set boundary conditions for the parallel plate capacitor.
7
8 Parameters
9 ----------
10 system_matrix_gg : numpy.ndarray
11 System matrix. The system matrix is modified by a call
12 to this function
13 rhs_g : numpy.ndarray
14 Right-hand side vector. The right-hand side vector is
15 modified by a call to this function.
16 top_left : int
17 Leftmost node of the top electrode
18 top_right : int
19 Rightmost node of the top electrode
20 top_potential : float
21 Electrostatic potential of the top electrode
22 bottom_left : int
23 Leftmost node of the bottom electrode
24 bottom_right : int
25 Rightmost node of the bottom electrode
26 bottom_potential : float
27 Electrostatic potential of the bottom electrode
28 nb_nodes : tuple of ints
29 Number of nodes in the Cartesian directions
30 """
31 Nx, Ny = nb_nodes
32 # Dirichlet boundary conditions for top plate
33 for i in range(top_left, top_right+1):
34 n = node_index(i, Ny-1, nb_nodes)
35 mat_g = np.zeros(Nx*Ny)
36 mat_g[n] = 1
37 system_matrix_gg[n] = mat_g
38 rhs_g[n] = top_potential
39
40 # Dirichlet boundary conditions for bottom plate
41 for i in range(bottom_left, bottom_right+1):
42 n = node_index(i, 0, nb_nodes)
43 mat_g = np.zeros(Nx*Ny)
44 mat_g[n] = 1
45 system_matrix_gg[n] = mat_g
46 rhs_g[n] = bottom_potential
Der gesamte Simulationscode enthält nun Aufrufe dieser Funktionen, gefolgt von der numerischen Lösung des linearen Gleichungssystems:
2system_matrix_gg = assemble_system_matrix(element_matrix_ll,
3 nb_nodes)
4
5# Boundary conditions
6capacitor_bc(system_matrix_gg, rhs_g,
7 top_left, top_right, top_potential,
8 bottom_left, bottom_right, bottom_potential,
9 nb_nodes)
10
11# Solve system of linear equations
12potential_g = np.linalg.solve(system_matrix_gg, rhs_g)
Die Variable potential_g enthält nun die Werte des elektrostatischen Potentials auf den Knoten.
11.5 Visualisierung
Das Ergebnis der Rechnung kann mit Hilfe der matplotlib-Bibliothek visualisiert werden. Die Funktion matplotlib.pyplot.tripcolor kann Daten auf einem triangulierten 2D-Gitter darstellen. Der folgende Codeblock visualisiert das Ergebnis der Simulation mit Hilfe dieser Funktion.
2import matplotlib.tri
3
4def make_grid(nb_nodes):
5 """
6 Make an array that contains all elements of the grid. The
7 elements are described by the global node indices of
8 their corners. The order of the corners is in order of
9 the local node index.
10
11 They are sorted in geometric positive order and the first
12 is the node with the right angle corner at the bottom
13 left. Elements within the same box are consecutive.
14
15 This is the first element per box:
16
17 2
18 | \
19 | \
20 dy | \
21 | \
22 0 --- 1
23
24 dx
25
26 This is the second element per box:
27
28 dx
29 1 ---0
30 \ |
31 \ | dy
32 \ |
33 \|
34 2
35
36 Parameters
37 ----------
38 nb_nodes : tuple of ints
39 Number of nodes in the Cartesian directions
40
41 Returns
42 -------
43 triangles_el : numpy.ndarray
44 Array containing the global node indices of the
45 element corners. The first index (suffix _e)
46 identifies the element number and the second index
47 (suffix _l) the local node index of that element.
48 """
49 Nx, Ny = nb_nodes
50 # These are the node position on a subsection of the grid
51 # that excludes the rightmost and topmost nodes. The
52 # suffix _G indicates this subgrid.
53 y_G, x_G = np.mgrid[:Ny-1, :Nx-1]
54 x_G.shape = (-1,)
55 y_G.shape = (-1,)
56
57 # List of triangles
58 lower_triangles = np.vstack(
59 (node_index(x_G, y_G, nb_nodes),
60 node_index(x_G+1, y_G, nb_nodes),
61 node_index(x_G, y_G+1, nb_nodes)))
62 upper_triangles = np.vstack(
63 (node_index(x_G+1, y_G+1, nb_nodes),
64 node_index(x_G, y_G+1, nb_nodes),
65 node_index(x_G+1, y_G, nb_nodes)))
66 # Suffix _e indicates global element index
67 return np.vstack(
68 (lower_triangles, upper_triangles)).T.reshape(-1, 3)
69
70def plot_results(values_g, nb_nodes, mesh_style=None,
71 ax=None):
72 """
73 Plot results of a finite-element calculation on a
74 two-dimensional structured grid using matplotlib.
75
76 Parameters
77 ----------
78 nb_nodes : tuple of ints
79 Number of nodes in the Cartesian directions
80 values_g : array_like
81 Expansion coefficients (values of the field) on the
82 global nodes
83 mesh_style : str, optional
84 Will show the underlying finite-element mesh with
85 the given style if set, e.g. ’ko-’ to see edges
86 and mark nodes by points
87 (Default: None)
88 ax : matplotlib.Axes, optional
89 Axes object for plotting
90 (Default: None)
91
92 Returns
93 -------
94 trim : matplotlib.collections.Trimesh
95 Result of tripcolor
96 """
97 Nx, Ny = nb_nodes
98
99 # These are the node positions on the full global grid.
100 y_g, x_g = np.mgrid[:Ny, :Nx]
101 x_g.shape = (-1,)
102 y_g.shape = (-1,)
103
104 # Gouraud shading linearly interpolates the color between
105 # the nodes
106 if ax is None:
107 ax = plt
108 triangulation = matplotlib.tri.Triangulation(
109 x_g, y_g, make_grid(nb_nodes))
110 c = ax.tripcolor(triangulation, values_g,
111 shading=’gouraud’)
112 if mesh_style is not None:
113 ax.triplot(triangulation, mesh_style)
114 return c
115
116plt.subplot(111, aspect=1)
117plot_results(potential_g, nb_nodes, show_mesh=True)
118plt.xlabel(r’$x$-position ($\Delta x$)’)
119plt.ylabel(r’$y$-position ($\Delta y$)’)
120plt.colorbar().set_label(r’Potential $\Phi$ (V)’)
121plt.tight_layout()
122plt.show()
Die Funktion make_grid erzeugt hier eine Liste der globalen Knotenindices pro Element. Der erste Index ist der Index des Elements (Suffix e), der zweite Index ist der lokale Knotenindex innerhalb des Elements (Suffix l). Die Knoten des jeweiligen Elements sind gegen den Uhrzeigersinn nummeriert. Für die Visualisierung wird “Gouraud”-Schattierung genutzt. Diese Art der Färbung interpoliert den Wert der Knoten linear auf den Dreiecken und entspricht exakt der Interpolationsvorschrift unserer Formfunktionen. Wir können damit die volle interpolierte Funktion \(\Phi _N(\v {r})\) darstellen.
11.6 Beispiel: Plattenkondensator
Mit Hilfe des hier entwickelten Codes kann nun das elektrostatische Potential innerhalb eines Plattenkondensators berechnet werden. Abbildung 11.2 zeigt das Ergebnis dieser Rechnung für unterschiedliche Auflösung der Simulation, also unterschiedliche Anzahl an Elementen. Durch Erhöhung der Auflösung kann die Simulation systematisch verbessert werden.
Für die Berechnung der Kapazität müssen wir nun noch die Ladung auf den Kondensatorplatten ermitteln. Die Gesamtladung \(Q_\alpha \) auf der Elektrode \(\alpha \) erhält man aus der Oberflächenladung, die durch Gl. \eqref{eq:surfacecharge} gegeben ist. Durch Integration über die Fläche der Kondensatorplatten \(A_\alpha \) erhält man \begin {equation} Q_\alpha = \int _{A_\alpha } \dif ^2 r\, \sigma (\v {r}) = \varepsilon \int _{A_\alpha } \dif ^2 r\, \nabla \Phi _N\cdot \hat {n}(\v {r}). \end {equation} Hier spielt nun die Permittivität \(\varepsilon \) eine wichtige Rolle für die Einheit der Ladung. Wir können nun wieder die Reihenentwicklung einsetzen. Zum Integral trägt nur Elementtyp \((1)\) bei, und hier nur die Formfunktionen, bei denen die Ableitung in \(y\)-Richtung nicht verschwindet, da \(\nabla \Phi _N\cdot \hat {n}(\v {r})=\pm \partial \Phi _N/\partial y\). Das Vorzeichnen ist bei oberer und unterer Kondensatorplatte umgedreht. Nicht-verschwindende Beiträge kommen von den Formfunktionen \(N_0^{(1)}\) und \(N_2^{(1)}\). Man erhält \begin {align} \int _0^{\Delta x} \dif x \frac {\partial N_0^{(1)}}{\partial y} &= \int _0^{\Delta x} \dif x \frac {1}{\Delta y} = \frac {\Delta x}{\Delta y} \\ \int _0^{\Delta x} \dif x \frac {\partial N_2^{(1)}}{\partial y} &= \int _0^{\Delta x} \dif x \left (-\frac {1}{\Delta y}\right ) = -\frac {\Delta x}{\Delta y} \end {align}
und damit für \(\Delta x=\Delta y\) \begin {equation} Q^{(n)} = \varepsilon t(a_0 - a_2) \end {equation} als Beitrag des Elements \((n)\) zur Ladung auf der Elektrode. Hierbei bezeichnen die Indices der Koeffizienten \(a_0\) und \(a_2\) die jeweiligen lokalen Knotenindices. Die Größe \(t\) ist die Tiefe der Simulationsdomäne. Da wir das Problem hier in zwei Dimensionen betrachten sind alle Ladungen effektiv Linienladungen (pro Tiefe) und der Faktor \(t\) wird benötigt, um auf eine absolute Ladung zu kommen. Unser Plattenkondensator ist in die dritte Dimension unendlich lang. Der Faktor \(\varepsilon t\) hat die Einheit Farad und ist damit eine Kapazität.
Die Kapazität des Kondensators ist nun gegeben als \(C=Q_0/\Delta \Phi \), wobei \(Q_0\) nun die Ladung auf einer Kondensatorplatte ist und \(\Delta \Phi \) der (vorgegebene) Potentialunterschied. Die zweite Kondensatorplatte muss die Ladung \(Q_1=-Q_0\) tragen. Der Code für die Berechnung der Ladung auf den Kondensatorplatten sieht daher folgendermaßen aus:
2 top_left, top_right,
3 bottom_left, bottom_right):
4 """
5 Compute charge on both capacitor plates.
6
7 Parameters
8 ----------
9 potential_g : array_like
10 Electrostatic potential
11 nb_nodes : tuple of ints
12 Number of nodes in the Cartesian directions
13 top_left : int
14 Leftmost node of the top electrode
15 top_right : int
16 Rightmost node of the top electrode
17 bottom_left : int
18 Leftmost node of the bottom electrode
19 bottom_right : int
20 Rightmost node of the bottom electrode
21
22 Returns
23 -------
24 charge_top : float
25 Charge (divided by permittivity and thickness) on top
26 plate
27 charge_bottom : float
28 Charge (divided by permittivity and thickness) on
29 bottom plate
30 """
31 Nx, Ny = nb_nodes
32 charge_top = 0.0
33 for i in range(top_left+1, top_right+1):
34 charge_top += \
35 potential_g[node_index(i, Ny-1, nb_nodes)] - \
36 potential_g[node_index(i, Ny-2, nb_nodes)]
37
38 charge_bottom = 0.0
39 for i in range(bottom_left+1, bottom_right+1):
40 charge_bottom += \
41 potential_g[node_index(i, 0, nb_nodes)] - \
42 potential_g[node_index(i, 1, nb_nodes)]
43
44 return charge_top, charge_bottom
Natürlich wissen wir, wie die Kapazität eines Plattenkondensators aussieht. Sie ist gegeben durch \begin {equation} C = \varepsilon \frac {A}{d}, \label {eq:anacapacity} \end {equation} wobei \(A=tL\) die Fläche der Kondensatorplatte ist und \(d\) der Abstand der Platten. (\(L\) ist die Länge der Platten, siehe Abb. 11.1a.) Dies können wir entdimensionalisiert als \begin {equation} \frac {C}{\varepsilon t} = \frac {L}{d} \end {equation} schreiben. Die linke Seite erhalten wir direkt aus unserer Simulation. Das Ergebnis der Rechnung mit finiten Elementen ist in Abb. 11.3 im Vergleich mit diesem analytischen Ausdruck gezeigt. Man sieht, dass der analytische Ausdruck nur bei kleinen Aspektverhältnissen \(d/L<1\) gilt. Die Herleitung dieses Ausdrucks nimmt an, dass die Feldlinien überall parallel und senkrecht zu den Kondensatorplatten verlaufen. Für große Abstände der Kondensatorplatten ist dies nicht mehr der Fall und Streufelder am Rand der Platten fangen an, eine Rolle für die Kapazität zu spielen. Diese sind nicht von Gl. \eqref{eq:anacapacity} erfasst, werden aber in der Simulation abgebildet.
Anmerkung: Die Systemmatrix der finite-Elemente Methode ist dünnbesetzt (engl. “sparse”). Für dünnbesetzte Matrizen gibt es spezielle Datenstrukturen, die den Umgang mit diesen Matrizen vereinfachen. Diese sind in dem Paket scipy.sparse implementiert. Wir können diese Routinen nutzen, um eine dünnbesetzte Systemmatrix zu konstruieren:
2
3def assemble_system_matrix(element_matrix_ll, nb_nodes):
4 """
5 Assemble system matrix from the element matrix
6
7 Parameters
8 ----------
9 element_matrix_ll : array_like
10 3 x 3 element matrix
11 nb_nodes : tuple of ints
12 Number of nodes in the Cartesian directions
13
14 Returns
15 -------
16 system_matrix_gg : numpy.ndarray
17 System matrix
18 """
19 Nx, Ny = nb_nodes
20
21 # Compute grid
22 grid_el = make_grid(nb_nodes)
23
24 # Get number of elements
25 nb_elements, nb_corners = grid_el.shape
26
27 # Spread out grid and element matrix such that they can
28 # be used as global node coordinates for the sparse
29 # matrix
30 grid1_ell = np.stack(
31 [grid_el, grid_el, grid_el], axis=1)
32 grid2_ell = np.stack(
33 [grid_el, grid_el, grid_el], axis=2)
34 element_matrix_ell = np.stack(
35 [element_matrix_ll]*nb_elements, axis=0)
36
37 # Construct sparse system matrix
38 # ‘coo_matrix‘ will automatically sum duplicate entries
39 system_matrix_gg = coo_matrix(
40 (element_matrix_ell.reshape(-1),
41 (grid1_ell.reshape(-1), grid2_ell.reshape(-1))),
42 shape=(Nx*Ny, Nx*Ny))
43
44 return system_matrix_gg.todense()
Diese Methode ersetzt die obige Implementation von assemble_system_matrix. Sie liefert (aus Gründen der Kompatibiltät zum Rest der hier gezeigten Implementierung) zum Schluss wieder eine dichtbesetzte (engl. “dense”) Matrix, man kann aber durchaus mit der dünnbesetzten Matrix weiterrechnen. Im Rahmen der Anwendung von coo_matrix werden hier die globalen Knotenindizes als “Koordinaten” der Matrixeinträge eingesetzt. Hierzu müssen sowohl die Knotenindizes als auch die Einträge der Elementmatrix auf die Größe der Systemmatrix vervielfältigt werden. Dies geschieht durch die numpy.stack Befehle in diesen Codefragment.