Kapitel 14
Nichtlineare Probleme

14.1 Newton-Raphson-Verfahren

Das Newton-Raphson-Verfahren, oder auch kurz nur Newton-Verfahren, ist ein Verfahren für die iterative Lösung einer nichtlinearen Gleichung. Zur Illustration beschreiben wir dieses hier zunächst für skalarwertige Funktionen und werden dann das Verfahren für vektorwertige Funktionen verallgemeinern.

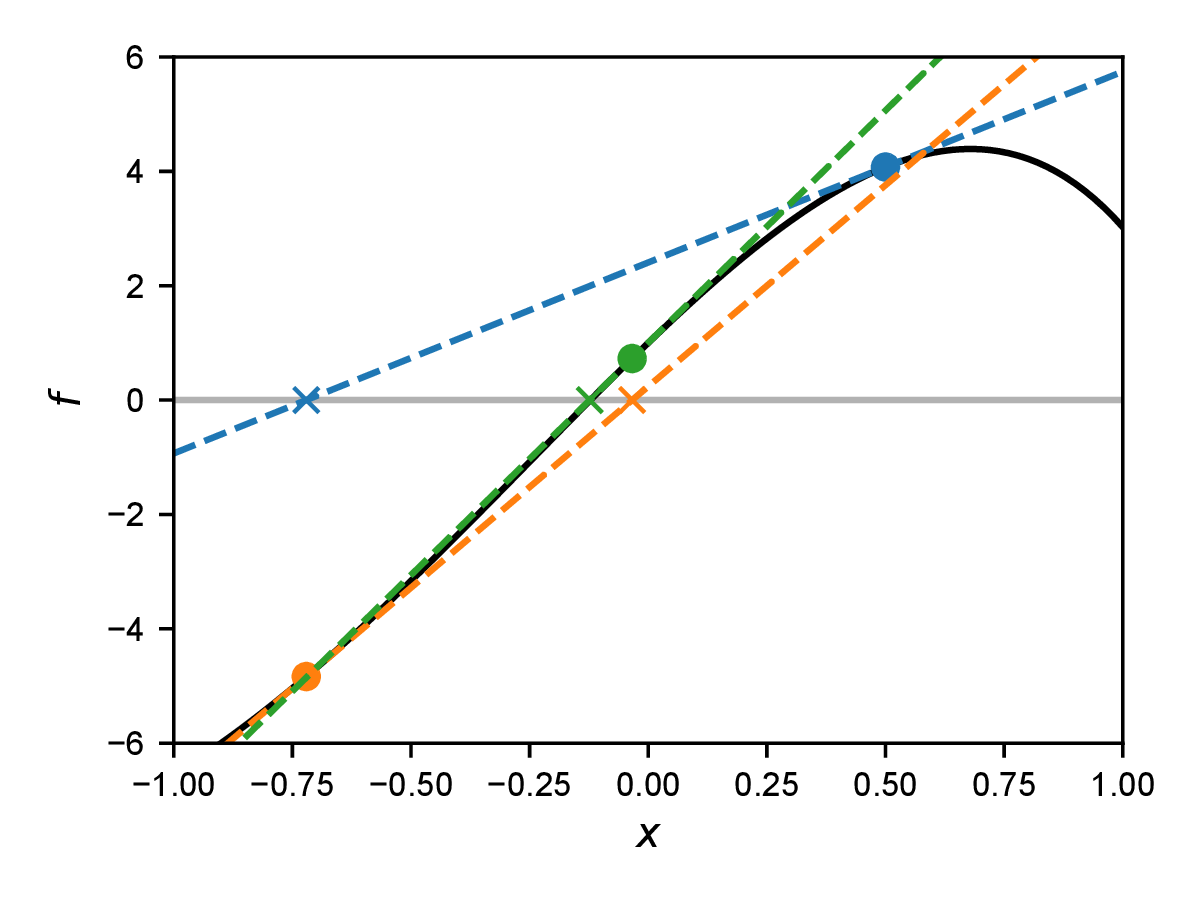
Wir suchen die allgemeine Lösung für die Gleichung \(f(x)=0\) mit beliebiger Funktion \(f(x)\). Die Idee des Newton-Verfahrens ist es nun, die Gleichung an einem Punkt zu linearisieren, also eine Taylorentwicklung bis zur ersten Ordnung hinzuschreiben, und dann dieses linearisierte System zu Lösen. Die um den Punkt \(x_i\) taylorentwickelte Gleichung \begin {equation} f(x) \approx f(x_i) + (x - x_i) f'(x_i) = 0 \label {eq:newtonapprox} \end {equation} hat die Lösung \begin {equation} x_{i+1} = x_i - f(x_i) / f'(x_i), \end {equation} wobei \(f'(x)=\dif f/\dif x\) die erste Ableitung der Funktion \(f\) ist. Der Wert \(x_{i+1}\) ist nun (unter gewissen Bedingungen) näher an der Nullstelle \(x_0\) (mit \(f(x_0)=0\)) als der Wert \(x_i\). Die Idee des Newton-Verfahrens ist es nun, eine Folge \(x_i\) von linearen Approximationen der Funktion \(f\) zu konstruieren, die auf die Nullstelle konvergiert. Wir nutzen also die Nullstelle der linearisierten Form der Gleichung als Startpunkt für die nächste Iteration. Ein Beispiel einer solchen Iteration ist in Abb. 14.1 gezeigt.

Die Diskretisierung unserer PDGLs führte uns auf ein lineares Gleichungssystem, welches wir Abstrakt als \(\v {f}(\v {x})=\v {0}\) schreiben können. Wir werden in diesem Kapitel nichtlineare Gleichungssysteme dieser Form kennen lernen. Das Newton-Verfahren für die Lösung solcher gekoppelter nichtlinearer Gleichungen funktioniert analog zu dem skalaren Fall. Wir schreiben zunächst die Taylor-Entwicklung \begin {equation} \v {f}(\v {x}) \approx \v {f}(\v {x}_i) + \t {K}(\v {x}_i)\cdot (\v {x} - \v {x}_i) = 0 \label {eq:newtonapproxmultidim} \end {equation} mit der Jacobi-Matrix \begin {equation} K_{mn}(\v {x})=\frac {\dif f_m(\v {x})}{\dif x_n}. \end {equation} Im Kontext der finiten Element wird \(\t {K}(\v {x}_i)\) auch häufig die Tangentenmatrix (engl. “tangent matrix” oder “tangent stiffness matrix”) genannt. Das Newton-Verfahren lässt sich dann als \begin {equation} \v {x}_{i+1} = \v {x}_i - \t {K}^{-1}(\v {x}_i)\cdot \v {f}(\v {x}_i) \label {eq:newtonmultidim} \end {equation} schreiben. In der numerischen Lösung von Gl. \eqref{eq:newtonmultidim} wird der Schritt \(\Delta \v {x}_i = \v {x}_{i+1} - \v {x}_i\) meist über die Lösung des linearen Gleichungssystems \(\t {K}_i\cdot \Delta \v {x}_i = -\v {f}(\v {x}_i)\) und nicht mit Hilfe einer expliziten Matrixinversion von \(\t {K}_i\) implementiert.

Für ein rein lineares Problem, wie wir sie ausschließlich in den vorhergehenden Kapiteln besprochen haben, ist die Tangentenmatrix \(\t {K}\) konstant und nimmt die Rolle der Systemmatrix ein. In diesem Fall konvergiert die Newton-Iteration in einem Schritt.

14.2 Numerische Integration

Alle Integrale aus den vorhergehenden Kapiteln, insbesondere die Integrale der Laplace- und Massematrizen, konnten vollständig analytisch gelöst werden. Dies ist bei nichtlinearen PDGLs in vielen Fällen nicht mehr möglich. Wir müssen daher über numerische, approximative Integration reden. Dies wird oft synonym auch numerische Quadratur genannt. Wir werden hier die Terme Integration und Quadratur austauschbar verwenden.

Wir betrachten zunächst eine Funktion \(f(x)\) und möchten das Integral \(\int _{-1}^1 \dif x\, f(x)\) über ein gewisses Gebiet \([-1,1]\) auswerten. (Wir beschränken uns hier auf dieses Gebiet. Eine Integration über ein allgemeines Interval \([a,b]\) kann immer auf dieses Gebiet abgebildet werden.) Eine naheliegende Lösung wäre die Approximation des Integrals mit einer Summe von Rechtecken. Wir schreiben \begin {equation} \int _{-1}^1 \dif x\, f(x) \approx \sum _{n=0}^{N-1} w^\text {Q}_n f(x^\text {Q}_n), \label {eq:quadrature} \end {equation} wobei \(\sum _n w_n = 2\). Der Quadraturpunkt \(x_n^\text {Q}\) muss im \(n\)-ten Interval liegen, \(\sum _{i=0}^{n-2} w_i^\text {Q} - 1 < x_n^\text {Q} < \sum _{i=0}^{n-1} w_i^\text {Q}-1\). Gleichung \eqref{eq:quadrature} ist eine Quadraturregel (engl. “quadrature rule”). Die Punkte \(x_n^\text {Q}\) heißen Quadraturpunkte (engl. “quadrature points”) und die \(w_n^\text {Q}\) sind die Quadraturgewichte (engl. “quadrature weights”). Für die Rechteckregel sind diese Gewichte genau die Breite der Rechtecke, andere Formen einer Quadraturregel werden im Folgenden besprochen.

Wir stellen nun die Frage, welche Wahl von \(x_n^\text {Q}\) und \(w_n^\text {Q}\) für eine gegebene Zahl an Quadraturpunkten \(N\) ideal wäre. Eine gute Wahl für \(N=1\) ist sicherlich \(x_1^\text {Q}=0\) und \(w_1^\text {Q}=2\). Diese Regel führt für lineare Funktionen zu der exakten Lösung. Verschieben wir den Quadraturpunkt \(x_1^\text {Q}\) an einen anderen Ort, so werden nur noch konstante Funktionen exakt approximiert.

Mit zwei Quadraturpunkten sollten wir daher ein Polynom dritter Ordnung exakt integrieren können. Wir können diese Punkte bestimmen, in dem wir die exakte Integration von Polynomen bis zu dritter Ordnung mit einer aus zwei Termen bestehenden Summe explizit verlangen: \begin {align} \int _{-1}^1 \dif x\, 1 &= 2 = w_1^\text {Q} + w_2^\text {Q} \\ \int _{-1}^1 \dif x\, x &= 0 = w_1^\text {Q} x_1^\text {Q} + w_2^\text {Q} x_2^\text {Q} \\ \int _{-1}^1 \dif x\, x^2 &= 2/3 = w_1^\text {Q} (x_1^\text {Q})^2 + w_2^\text {Q} (x_2^\text {Q})^2 \\ \int _{-1}^1 \dif x\, x^3 &= 0 = w_1^\text {Q} (x_1^\text {Q})^3 + w_2^\text {Q} (x_2^\text {Q})^3 \end {align}

Die Lösung dieser vier Gleichungen führt direkt zu \(w_1^\text {Q}=w_2^\text {Q}=1\), \(x_1^\text {Q}=1/\sqrt {3}\) und \(x_2^\text {Q}=-1/\sqrt {3}\). Für drei Quadraturpunkte erhält man mit einer identischen Konstruktion \(w_1^\text {Q}=w_3^\text {Q}=5/9\), \(w_2^\text {Q}=8/9\), \(x_1^\text {Q}=-\sqrt {3/5}\), \(x_2^\text {Q}=0\) und \(x_3^\text {Q}=\sqrt {3/5}\). Diese Art der numerischen Integration nennt sich Gauß-Quadratur.

Für Integrale über beliebige Intervale \([a,b]\) müssen wir die Quadraturregeln umskalieren. Man erhält durch Substitution \(y=(a+b+(b-a)x)/2\) \begin {equation} \int _a^b \dif y f(y) = \frac {b-a}{2} \int _{-1}^1 \dif x f(y(x)) \approx \frac {b-a}{2} \sum _{n=0}^{N-1} w_n^\text {Q} f(y(x_n^\text {Q})), \label {eq:scaledquad} \end {equation} wobei die Gewichte \(w_n^\text {Q}\) und die Quadraturpunkte \(x_n^\text {Q}\) für das Interval \([-1,1]\) berechnet sind. Quadraturpunkte und Gewichte findet man oft in tabellierter Form, z.B. auf Wikipedia.

14.3 Beispiel: Poisson-Boltzmann-Gleichung

Wir diskutieren nun die numerische Lösung der nichtlinearen Poisson-Boltzmann-(PB-)Gleichung für zwei Spezies, \begin {equation} \begin {split} \nabla ^2 \Phi &= - \frac {c^\infty }{\varepsilon } \left [ q_+ \exp \left (-\frac {q_+ \Phi }{k_B T}\right ) + q_- \exp \left (-\frac {q_- \Phi }{k_B T}\right ) \right ] \\ &= \frac {2\rho _0}{\varepsilon } \sinh \left ( \frac {|e| \Phi }{k_B T} \right ) \end {split} \end {equation} wobei \(\rho _0=|e|c^\infty \) die Referenzladungsdichte und \(q_+=|e|\) and \(q_-=-|e|\) die ionischen Ladungen sind. Da für kleine \(x\) gilt \(\sinh x\approx x\), ist die linearisierte Variante der PB-Gleichung \(\nabla ^2\Phi =\Phi /\lambda ^2\) mit der Debye-Länge \(\lambda =\sqrt {\varepsilon k_B T/(2|e|\rho _0)}\). Wir können die Debye-Länge nutzen um die Gleichung zu \begin {equation} \tilde {\nabla }^2 \tilde {\Phi } = \sinh \tilde \Phi \label {eq:nondimensionalpb} \end {equation} mit dem entdimensionalisierten Potential \(\tilde {\Phi } = \varepsilon \tilde {\Phi }/(2\rho _0 \lambda ^2)\) und der entdimensionalisierten Länge \(\tilde {x}=x/\lambda \) (bzw. \(\dif /\dif \tilde {x}=\lambda \dif /\dif x\)) umzuschreiben. Im Folgenden werden wir mit Gl. \eqref{eq:nondimensionalpb} arbeiten aber der Einfachheit halber die Tilde nicht weiter explizit schreiben.

Wir betrachten nun die eindimensionale Variante der PB-Gleichung auf dem Interval \([0,L]\). Das Residuum ist \begin {equation} R(x) = \frac {\dif ^2 \Phi }{\dif x^2} - \sinh \Phi . \end {equation} Multiplikation mit einer Testfunktion \(v(x)\) liefert das gewichtete Residuum \begin {equation} \begin {split} (v, R) &= (v, \dif ^2 \Phi /\dif x^2) - (v, \sinh \Phi ) \\ &= \left . v\frac {\dif \Phi }{\dif x}\right |_0^L - \left (\frac {\dif v}{\dif x}, \frac {\dif \Phi }{\dif x}\right ) - (v, \sinh \Phi ). \end {split} \end {equation} Der rechte Term ist nichtlinear in \(\Phi \) und benötigt zur Lösung numerische Quadratur. Im Folgenden vernachlässigen wir weiterhin den Oberflächenterm.

Der nächste Schritt ist der Galerkin-Ansatz, \(\Phi (x)\approx \Phi _N(x) = \sum _{n=0}^N a_n \varphi _n(x)\) und \(v(x)=\varphi _k(x)\). Das Residuum für Basisfunktion \(k\) wird zu \begin {equation} R_k = -(\dif \varphi _k/\dif x, \dif \Phi _N/\dif x) - (\varphi _k, \sinh \Phi _N). \end {equation} Den ersten Term identifizieren wir als den bekannten Laplace-Operator \begin {equation} (\dif \varphi _k/\dif x, \dif \Phi _N/\dif x) = L_{kn} a_n \end {equation} mit der bekannten (konstanten) Laplace-Matrix \(L_{kn}\). (Die Laplace-Matrix ist konstant, da der Laplace-Operator linear ist.) Den nichtlinearen Term \((\varphi _k,\sinh \Phi _N)\) nähern wir nun mit Hilfe von Gauß-Quadratur, \begin {equation} (\varphi _k,\sinh \Phi _N) = \sum _{ei} \frac {\Delta x^{(e)}}{2} w_i^\text {Q} \varphi _k(x_i^{(e)}) \sinh \Phi _N(x_i^{(e)}). \end {equation} Die Summe hier läuft über alle Elemente \(e\) und für jedes Element über die Quadraturpunkte \(i\) innerhalb dieses Elements. Weiterhin ist \(\Delta x^{(k)}\) die Länge des \((k)\)-ten Elements; der Term \(\Delta x^{(k)}/2\) kommt aus der Umskalierung der Quadraturregel, Gl. \eqref{eq:scaledquad}. Die Koeffizienten \(a_n\) tauchen in dieser Gleichung implizit im Potential \(\Phi _N\) auf. Das diskretisierte Residuum lautet daher \begin {equation} R_k = -L_{kn} a_n - \sum _{ei} \frac {\Delta x^{(e)}}{2} w_i^\text {Q} \varphi _k(x_i^{(e)}) \sinh \Phi _N(x_i^{(e)}). \end {equation} Wir suchen nun die Koeffizienten \(a_n\) für die \(R_k=0\). Damit wir das Newton-Verfahren dazu nutzen können, müssen wir noch die Tangentenmatrix bestimmen.

Hierzu linearisieren wir \(R_k\) in \(a_n\) um einen Referenzzustand \(\mathring {a}_n\), der den aktuellen Zustand der Newton-Iteration repräsentiert, siehe Gl. \eqref{eq:newtonapproxmultidim}. Man erhält \begin {equation} \left .\frac {\partial R_k}{\partial a_n}\right |_{\mathring {a}_n} = -L_{kn} - \sum _{ei} \frac {\Delta x^{(e)}}{2} w_i^\text {Q} \varphi _k(x_i^{(e)}) \varphi _n(x_i^{(e)}) \cosh \left . \Phi _N(x_i^{(e)}) \right |_{\mathring {a}_n}. \end {equation} Der zweite Term hat eine Struktur ähnlich der Massematrix und wir schreiben \begin {equation} M_{kn} = \sum _{ei} \frac {\Delta x^{(e)}}{2} w_i^\text {Q} \varphi _k(x_i^{(e)}) \varphi _n(x_i^{(e)}) \cosh \Phi _N(x_i^{(e)}), \label {eq:massmatrixnonlinear} \end {equation} wobei nun der Referenzzustandes \(\tilde {\v {s}}\) nicht mehr explizit angeben wurde. Die gesamte Tangentenmatrix ist daher \(\t {K}=-\t {L}-\t {M}\), wobei \(\t {M}\) explizit vom Zustand der Newton-Iteration abhängt. Für ein rein lineares Problem ist \(\t {K}\) die Systemsteifigkeitsmatrix.

Wir müssen nun \(M_{kn}\) bestimmen. Hierzu schreiben wir zunächst Gl. \eqref{eq:massmatrixnonlinear} in eine Elementmatrix um, \begin {equation} M_{IJ}^{(k)} = \frac {\Delta x^{(k)}}{2} \sum _i w_i^\text {Q} N_I^{(k)}(x_i^{(k)}) N_J^{(k)}(x_i^{(k)}) \cosh \Phi _N(x_i^{(k)}), \end {equation} wobei die globale Steifigkeitsmatrix \(M_{kn}\) wieder durch die übliche Prozedur “assembliert” werden kann.

14.3.1 Ein Quadraturpunkt

Besonders einfach wird dieser Ausdruck für Integration mit lediglich einem Gaußschen Quadraturpunkt. Dann gilt \(w_0^\text {Q}=2\) und \(x_0^{(k)}\) liegt genau in der Mitte des jeweiligen Elements, so dass \(N_I^{(k)}(x_0^{(k)})=1/2\). Man erhält \begin {equation} M_{IJ}^{(k)} = \frac {\Delta x^{(k)}}{4} \cosh \left ( \frac {a_I^{(k)} + a_J^{(k)}}{2} \right ). \label {eq:PBtangentonequad} \end {equation} Wir schauen uns nun wiederum den linearisierten Fall an. Die Linearisierung ergibt \(\cosh x\approx 1\) und Gl. \eqref{eq:PBtangentonequad} wird damit unabhängig von \(\v {a}\). Das Newton-Verfahren würde also in einem Schritt konvergieren; die Gleichung ist linear.

14.3.2 Zwei Quadraturpunkte

Für zwei Quadraturpunkte erhält man \begin {equation} \begin {split} M_{IJ}^{(k)} =& \frac {\Delta x^{(k)}}{2} \left \{ N_I^{(k)}(x_0^{k}) N_J^{(k)}(x_0^{(k)}) \cosh \Phi _N(x_0^{(k)}) \right . \\ & \left . \qquad \qquad + N_I^{(k)}(x_1^{k}) N_J^{(k)}(x_1^{(k)}) \cosh \Phi _N(x_1^{(k)}) \right \}. \end {split} \end {equation} Mit \(N_0^{(k)}(x_0^{(k)})=(3-\sqrt {3})/6\), \(N_1^{(k)}(x_0^{(k)})=(3+\sqrt {3})/6\), \(N_0^{(k)}(x_1^{(k)})=(3+\sqrt {3})/6\) und \(N_1^{(k)}(x_1^{(k)})=(3-\sqrt {3})/6\) wird dies zu \begin {equation} M_{IJ}^{(k)} = \frac {\Delta x^{(k)}}{12} \left \{ \cosh \Phi _N(x_0^{(k)}) + \cosh \Phi _N(x_1^{(k)}) \right \} \end {equation} für \(I\not =J\) und \begin {equation} M_{00}^{(k)} = \frac {\Delta x^{(k)}}{12} \left \{ \frac {6-\sqrt {3}}{3} \cosh \Phi _N(x_0^{(k)}) + \frac {6+\sqrt {3}}{3} \cosh \Phi _N(x_1^{(k)}) \right \} \end {equation} sowie \begin {equation} M_{11}^{(k)} = \frac {\Delta x^{(k)}}{12} \left \{ \frac {6+\sqrt {3}}{3} \cosh \Phi _N(x_0^{(k)}) + \frac {6-\sqrt {3}}{3} \cosh \Phi _N(x_1^{(k)}) \right \}. \end {equation} In linearisierten Fall erhält man \begin {equation} \t {M}^{(k)} = \Delta x^{(k)} \begin {pmatrix} 1/3 & 1/6 \\ 1/6 & 1/3 \end {pmatrix}, \end {equation} der exakten Massematrix für den linearen Fall.

Literaturverzeichnis

---