scipy: Optimization and root finding

Learning goals:

Solving equations numerically

SciPy

SciPy is a vast treasure trove of numerical methods for Python, for instance for optimisation (scipy.optimize), spectral analysis (scipy.fftpack), further linear algebra (scipy.linalg) and much more.

We will use SciPy extensively in the future exercise sessions, but we will not present a systematic overview over its capabilities, because they are too vast. However, the documentation is very good should help you along the way.

Example problem: Solving transcendental equations

Consider a pendulum with an angular spring that pulls the it towards a horizontal position.

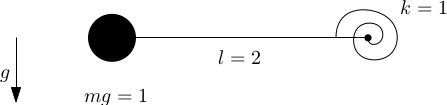
horizontal pendulum

Its equlibrium position is given by the following transcendental equation ($\varphi$ is the counter clock-wise angle between the pendulum and the horizon) $\varphi = 2\, \cos \varphi$

While this cannot be solved exactly, it is easily solved approximately using the SciPy optimisation module. First, we express the equation as a function of which the root is to be computed $f(x) = x-2\, \cos x,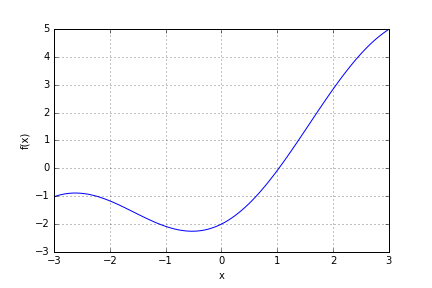$ fun_plot and then we use scipy.optmimize.root with a suitable initial guess x0 to find our solution.

import numpy as np
import scipy.optimize as optim
def fun(x):
    return x - 2*np.cos(x)

sol = optim.root(fun, x0 = 0)
print("root of f(x): x =", sol.x)

root of f(x): x = [1.02986653]

This example shows how simply even complicated problems (here the appriximative solution to a non-linear equation) can be solved without writing your own code by leveraging existing ScyPy functions.

Tasks

Read the help for root to understand what parameters it takes, and what information can be retrieved from the result
What happens if you set the initial guess $x_0 = -1.5$. Explain why the solver fails (Hint, look at the plot of the function).
Have a look at the documentation of scipy.optimize. How can you find the minimum of $f(x)$? What minimum do you find exactly?