Boundary conditions

Boundary Conditions for the Lattice Boltzmann Method

Boundary and initial conditions are an essential part of the LBM algorithm and their implementation should be placed in the proper position inside the solution scheme. In particular we will lay the emphasis on the difference between the pre-streaming probability density function \(f_i^{\star}\) and its value after the streaming \(f_i\).

As marked by several authors on literature [1,2], the streaming and the collision\(^1\) can be applied in both orders. Nonetheless the important thing is that the boundary condition describe how the streaming part takes place at the boundary, in other words the propagation of \(f_i\) at the boundary node is influenced by the boundary condition and its implementation needs to be treated differently then the pure streaming\(^2\).

\(^1\)Streaming and collision are also called propagation and relaxation respectively.
\(^2\)In the usual implementation of LBM the stream operation is applied also at the boundary nodes and then it is corrected right after by a boundary condition routine.

The main concept in implementing the boundary conditions in the LBM is that we don’t impose the conditions directly the physical variables \(\rho\) and \(\mathbf{u}\) at the boundary, but the probability density function \(f_i\).

There are two main groups of boundary condition for the LBM: - dry-node or link-wise: where the boundaries are located on the link between nodes. - wet-node: where the boundaries are placed on the lattice nodes.

In this course we will only on the dry-node group, since it is easier to be implemented and they retain a second order accuracy as long as the physical wall is placed exactly halfway between the nodes. With dry-node boundary conditions the external contour of the physical domain remains half cell outside the computational domain, as shown in figure 1. This is important to remember, since the evaluation of the simulated quantities on the external contour of the domain requires extrapolation of the results, as we will see, for example, in case of the no-slip wall condition.

Representation of the computational and physical domain with dry-node boundary conditions.

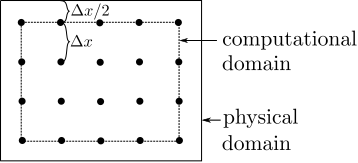
Periodic boundary conditions

The periodic boundary condition are used to implement symmetry conditions. In particular they describe a periodic flow where the fluid leaving a boundary re-enter the domain at the side. This condition is typically implicitly implemented during the streaming operation, where the populations \(f_i(\mathbf{x}+L,t)\) which leaves one border is automatically overwritten on the opposite border \(f_i(\mathbf{x},t)\). In terms of lattice nodes we can express this condition in the following way by using the notation shown in figure 2:

\[\begin{equation} f_i(\mathbf{x}_1,t) = f_i(\mathbf{x}_N,t). \end{equation}\] where \(\mathbf{x}_1\) and \(\mathbf{x}_N\) are the first and the last node in the physical domain, respectively.

Representation of the periodic boundary conditions without extra nodes.

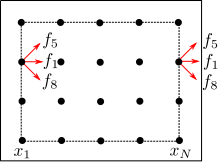
This condition is valid, for example, for the inlet/outlet of a Couette flow, where the flow is driven by the movement of one of the two walls (through the moving wall condition shown in the following sections).

Rigid wall

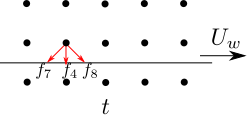
The presence of a rigid wall is modelled by defining the back bouncing populations \(f_i\) for the nodes on the computational domain. For example, in the case of the lower wall in a 2D geometry 4 we want to determine the population in the upwards channel \(f_6\),\(f_2\) and \(f_5\) which contain the information about the presence of a wall at the new time step \(t+\Delta t\). This is done by assuming that the population of the downwards channel \(f_7\),\(f_4\) and \(f_8\), which hit the wall at the time \(t\), is perfectly bounced back within on time step \(\Delta t\) to the upwards channel.

Schematic representation of the wall boundary condition with dry-node

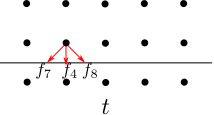
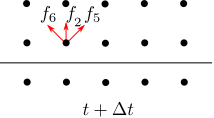
More generally we can say that the population which leaves the boundary node \(\mathbf{x}_b\) at \(t\) hit the wall at \(t+\Delta t\) and reach the opposite channel of the boundary node at \(t\). Therefore, for the populations which leave the boundary node the streaming operation is replaced by:

\[\begin{equation} f_{\bar{i}}(\mathbf{x}_b,t+\Delta t) = f_i^{\star}(\mathbf{x}_b,t). \label{eq:hard_wall} \end{equation}\]

Note: the index \({\bar{i}}\) denotes the opposite channel of \(i\) and \(f^{\star}\) denotes the value of the probability density function before the streaming step. So, e.g. \[\begin{equation} f_{6}(\mathbf{x}_b,t+\Delta t) = f_{8}^{\star}(\mathbf{x}_b,t). \label{eq:hard_wall_example} \end{equation}\]

moving wall

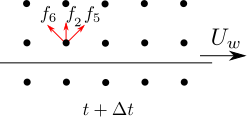
In the case of a moving wall, the bouncing back populations will gain or lose momentum during the interaction with the wall. In order to describe this change in the momentum we introduce a term to equation of the simple rigid wall case which is proportional to the wall velocity \(\mathbf{U}_w\).

\[\begin{equation} f_{\bar{i}}(\mathbf{x}_b,t+\Delta t) = f_i^{\star}(\mathbf{x}_b,t) - 2 w_i \rho_w \dfrac{\mathbf{c}_i \cdot \mathbf{u}_w}{c_s^2}. \label{eq:moving_wall} \end{equation}\]

where the subscript \(w\) denotes that the quantity is evaluated at the wall. This means that the value of the density \(\rho_w\) has to be extrapolated from the bulk or assumed to be equal to the average density \(\bar{\rho}\). In theb above equation the wall velocity is a vector \(\mathbf{u}_w\) but during this course we will consider only walls which move parallelly to their direction as shown in figure 5, since this condition ensure the mass conservation.

Note: Again, as with the rigid wall the index \({\bar{i}}\) denotes the opposite channel of \(i\) and \(f^{\star}\) denotes the value of the probability density function before the streaming step. So, e.g. \[\begin{equation} f_{6}(\mathbf{x}_b,t+\Delta t) = f_{8}^{\star}(\mathbf{x}_b,t) -2 w_8 \rho_w \dfrac{\mathbf{c}_8 \cdot \mathbf{u}_w}{c_s^2}. \label{eq:moving_wall_example} \end{equation}\]

Figure 5: Schematic representation of the moving wall boundary condition with dry-node. In this example the wall moves parallelly to its direction with velocity \(\mathbf{u}_w=U_w\).

Periodic boundary conditions with pressure gradient

Periodic boundary conditions can be also used in presence of a prescribed pressure variation \(\Delta p\) between the outlet and the inlet. This is the typical case of the flow in a pipe which is driven by the pressure difference between the inlet pressure \(p_{in}\) and the outlet one \(p_{out}\). Therefore we can express the periodic boundary condition as follows:

\[\begin{align} p(\mathbf{x},t) &= p(\mathbf{x}+L,t) + \Delta p, \\ \mathbf{u}(\mathbf{x},t) &= \mathbf{u}(\mathbf{x}+L,t). \end{align}\]

At this point it is important to note that in the LBM the pressure is directly related to the density through the ideal gas equation of state\(^3\):

\[\begin{equation} p = c_s^2 \rho. \end{equation}\]

with \(c_s^2 = 1/3\) in lattice units. This means that we are actually applying the following condition:

\[\begin{align} \rho(\mathbf{x},t) &= \rho(\mathbf{x}+L,t) + \Delta \rho, \\ \mathbf{u}(\mathbf{x},t) &= \mathbf{u}(\mathbf{x}+L,t). \label{eq:bc_pressure_def_rho} \end{align}\]

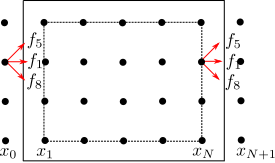
From the computational point of view we have to define a an extra layer of nodes outside the physical domain as shown in figure 3. If we think of the periodic conditions as many pipes connected one after each other, we can easily see that the extra node \(\mathbf{x}_0\) at the inlet corresponds to the last node \(\mathbf{x}_N\) which is still in the physical domain of the previous pipe. Therefore we can apply the periodic conditions by relating \(\mathbf{x}_N\) to its image node \(\mathbf{x}_0\) and consequently by relating \(\mathbf{x}_1\) to its image node \(\mathbf{x}_{N+1}\).

The boundary conditions have now to be applied on the probability density function which we can decompose in an equilibrium contribution \(f_i^{eq}(\rho,\mathbf{u})\) and a non equilibrium contribution \(f_i^{neq}(\rho,\mathbf{u})\). In order to apply the periodicity, for example, in the \(x\)-direction we have to impose that the variable at \(x_0\) are equal to those at \(x_N\) and do the same also for \(x_{N+1}\) and \(x_1\):

\[\begin{align} f_i^{eq}(x_0,y,t) = f_i^{eq}(\rho_{in},\mathbf{u}_N) \\ f_i^{eq}(x_{N+1},y,t) = f_i^{eq}(\rho_{out},\mathbf{u}_1) \end{align}\]

while for the non equilibrium part we can copy the value of the corresponding image node:

\[\begin{align} f_i^{neq}(x_0,y,t) = f_i^{neq}(x_N,y,t) \\ f_i^{neq}(x_{N+1},y,t) = f_i^{neq}(x_1,y,t). \end{align}\]

The non equilibrium populations have to be computed before the streaming: \(f_i^{neq} = f_i^{\star} - f_i^{eq}\).

Using this definition we can express the boundary conditions on the extra nodes:

\[\begin{align} f_i(x_0,y,t) &= f_i^{eq}(\rho_{in},\mathbf{u}_N) + \left( f_i^{\star}(x_N,y,t) - f_i^{eq}(x_N,y,t) \right) \\ f_i(x_{N+1},y,t) &= f_i^{eq}(\rho_{out},\mathbf{u}_1) + \left( f_i^{\star}(x_1,y,t) - f_i^{eq}(x_1,y,t) \right) \end{align}\]

with \(\rho_{out}=p_{out}/c_s^2\) and \(\rho_{in}=(p_{out} + \Delta p) /c_s^2\).

Figure 3: Representation of the periodic boundary conditions with extra nodes.

\(^3\)To be more precise: we are considering the flow of an incompressible fluid through the lattice Boltzmann equation which is an equation derived for a compressible fluid based on the ideal gas equation of state.

Inlet

The are several way to implement an inlet condition, in this section we analyse the most direct approach to assign a velocity and density profile at the inlet. The velocity \(\mathbf{u}_{in}\) and density \(\rho_{in}\) can be given as input at the inlet by directly assigning the equilibrium function \(f^{eq}\) at the boundary node \(\mathbf{x}_b\) in the following way:

\[\begin{equation} f_i(\mathbf{x}_b,t+\Delta t) = f_i^{eq}(\rho_{in}, \mathbf{u}_{in}) \label{eq:f_inlet} \end{equation}\]

where \(f_i^{\text{eq}}\) is the equilibrium function. It is important to notice, that the above inlet condition has to be applied to all the channels \(i\) and not only to the channels which point into the domain.

outlet

We have seen in the previous subsections that the unknown at any boundary is the population which enters the domain. The same holds also for the outlet boundary condition where we can extrapolate this information from the second last node \(\mathbf{x}_{b2}=\mathbf{x}_b-\Delta \mathbf{x}\) before the boundary node \(\mathbf{x}_b\):

\[\begin{equation} f_i(\mathbf{x}_b,t+\Delta t) = f_i(\mathbf{x}_{b2},t). \end{equation}\]

Where the index \(i\) denotes the channel pointing into the domain. Alternatively one can use a second order extrapolation scheme by exploiting the information in the third last node \(\mathbf{x}_{b3}=\mathbf{x}_b-2\Delta \mathbf{x}\):

\[\begin{equation} f_i(\mathbf{x}_b,t+\Delta t) = 2f_i(\mathbf{x}_{b2},t) -f_i(\mathbf{x}_{b3},t). \end{equation}\]

Video

References

[1] Krüger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G., & Viggen, E. M. (2017). The lattice Boltzmann method. Springer International Publishing, 10, 978-3.

[2] Succi, S., & Succi, S. (2018). The lattice Boltzmann equation: for complex states of flowing matter. Oxford University Press.