Lattice Boltzmann
The Boltzmann transport equation (BTE) was introduced by Ludwig Boltzmann in the context of kinetic gas theory (Boltzmann 1995) and is a statistical model for the transport of molecular constituents during flow (Cercignani 1988). The Lattice Boltzmann method (LBM) is a numerical scheme based on a discretized version of the BTE, introduced by McNamara and Zanetti (1988). LBM models have been used for the last three decades to study the dynamics of fluids in many different applications, from multiphase flow (A. K. Gunstensen et al. 1991; Grunau, Chen, and Eggert 1993), porous media (Aharonov and Rothman 1993; Andrew K. Gunstensen and Rothman 1993) to microfluidics (Zhang 2011). A thorough review of its applications in fluid dynamics and beyond can be found in Succi (2001).
Probabily density
Given the positions \(\mathbf r_i\) and velocities \(\mathbf v_i\) of a huge number \(N\) of molecules, we would have to solve a huge number of equations of motion \(\mathbf {\dot r}_i\) and \(\mathbf {\dot v}_i\). Indeed, this is what one will do in Molecular Dynamics Simulations.
Instead of following the trajectories of all the \(N\) particles in phase space, i.e. the space spanned by the \(2D \times N\) coordinates of positions and velocities, we take the average over an infinitesimal “volume” in phase space. Thus \(f(\mathbf v,\mathbf r,t)\) turns out to be a probability density for finding a molecule with velocity \(\mathbf{v}\) at position \(\mathbf{r}\) at the time \(t\). The 0th, 1st and 2nd moments of this probability density define the mass density \(\rho(\mathbf{r}, t)\), the momentum density \(\mathbf{j}(\mathbf{r}, t)\) and the temperature \(T(\mathbf{r}, t)\) respectively in \(D\)-dimensional space, \[ \begin{split} \rho(\mathbf{r}, t) &= m \int \mathrm{d}^Dv\, f(\mathbf{v},\mathbf{r},t) \\ \mathbf{j}(\mathbf{r}, t) &= \rho(\mathbf{r}, t)\mathbf{u}(\mathbf{r}, t) =m \int \mathrm{d}^Dv\, \mathbf{v} f(\mathbf{v},\mathbf{r},t) \\ k_B T(\mathbf{r}, t) &= \frac{m^2}{D \rho(\mathbf{r}, t)} \int \mathrm{d}^Dv\, \left[\mathbf{v}-\mathbf{u}(\mathbf{r}, t)\right]^2 f(\mathbf{v},\mathbf{r},t), \end{split} \tag{1}\] where we have assumed a monoatomic system with molecules of mass \(m\). We defined here the average velocity \(\mathbf{u}(\mathbf{r}, t)\) at position \(\mathbf{r}\). And \(k_B\) is the Boltzmann constant.
Watch the following video for a more thorough explanation. Note: in the video, the probability desnity is dentoed with position as its first argument.The Boltzmann transport equation
The BTE describes the temporal evolution of the probability density \(f(\mathbf{v},\mathbf{r},t)\), i.e. the total time-rate of change of this probability distribution, \(\mathrm{d}f/\mathrm{d}t\). We know that for large times \(t\) it must relax towards statistical equilibrium, given by the Maxwell velocity distribution function (Huang 1987), \[ f^\text{eq}(\mathbf{v}; \rho, \mathbf{u}, T) = \frac{\rho}{m} \left(\frac{m}{2\pi k_B T}\right)^{D/2} \exp\left\{-\frac{m(\mathbf{v}-\mathbf{u})^2}{2 k_B T}\right\}. \tag{2}\] A common approximation is to assume relaxation of \(f\) towards \(f^\text{eq}\) with a single characteristic time \(\tau\), as suggested by Bhatnagar, Gross, and Krook (1954), \[ \frac{\mathrm{d}f(\mathbf{v}, \mathbf{r}, t)}{\mathrm{d}t} = -\frac{f(\mathbf{v},\mathbf{r},t)-f^\text{eq}(\mathbf{v}; \rho(\mathbf{r}, t), \mathbf{u}(\mathbf{r}, t), T(\mathbf{r}, t))}{\tau}. \tag{3}\] Equation 3 is the BGK-Boltzmann equation. Note that the total derivative of \(f\) is \[\begin{split} \frac{\mathrm{d}f}{\mathrm{d}t} &=\mathbf{\dot v} \frac{\partial f(\mathbf{v},\mathbf{r},t)}{\partial \mathbf{v}}+ \mathbf{\dot r} \frac{\partial f(\mathbf{v},\mathbf{r},t)}{\partial \mathbf{r}} +\frac{\partial f(\mathbf{v},\mathbf{r},t)}{\partial t} \\ &=\frac{\mathbf{F}(\mathbf{r})}{m} \frac{\partial f(\mathbf{v},\mathbf{r},t)}{\partial \mathbf{v}}+ \mathbf{v}\frac{\partial f(\mathbf{v},\mathbf{r},t)}{\partial \mathbf{r}} +\frac{\partial f(\mathbf{v},\mathbf{r},t)}{\partial t}, \end{split}\]where \(\mathbf{F}(\mathbf{r})\) is an external force acting on the molecules.
We will remain within the context of this single (BGK) relaxation time approximation, but modern developments of the method aim at introducing multiple relaxation times, for example by relaxing the cumulants of \(f\) individually (M. Geier, Greiner, and Korvink 2006; Martin Geier et al. 2015).
The streaming part
Think of the probability density as some kind of density that is subject to transport. In fact the BTE is a transport equation transporting density of probability at a certain velocity in real space subject to the velocity itself. An acceleration will add transport of phase space density in velocity space as well. Both processes togehter will lead to a streaming of phase space density.
Watch the following video for a more thorough explanation. Note: in the video, the probability desnity is dentoed with position as its first argument.
The collision part
The r.h.s. term of the the BTE \(\left(\frac{\partial f}{\partial t}\right)_{coll}\) need futher explanation. The streaming part of the BTE, i.e. the l.h.s., just displaces the probability density in real and velocity space. What happens if two particles collide. Assume that it is an elastic scattering process conserving momentum and energy. This scattering process is assume to happen on a time scale much shorter that the time scale of the streaming process. Then we might model this process as an instantaneous exchange of energy and momentum between two particles. This is not a continuous process as the streaming part is because it comes in collision of very short duration. Thus it cannot be modelled as a differential equation leading to a continuous change.
Imagine there are myriads of such scattering processes going on. The single process lasts no longer that a fraction of a femtosecond. Thus it might be seen as instantaneous. N.B.: Molecular Dynamics would explicitely resolve such processes but only for a limitted number of particle with which we shall not be able to describe a decent amount of liquid. To this end we look at thes scattering processes in a probabilistic manner as well. The collision term thus looks like \[\left(\frac{\partial f}{\partial t}\right)_{coll}= \int\int\int w(\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3,\mathbf{v}) \left\{ f(\mathbf{x},\mathbf{v}_1,t) f(\mathbf{x},\mathbf{v}_2,t)- f(\mathbf{x},\mathbf{v}_3,t) f(\mathbf{x},\mathbf{v},t) \right\} \mathrm{d}\mathbf{v}_1\mathrm{d}\mathbf{v}_2\mathrm{d}\mathbf{v}_3 \] Let us motivate this term: * \(w(\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3,\mathbf{v})\) is the probability that two colliding particles with velocities \(\mathbf{v}_1\) and \(\mathbf{v}_2\) result in two outgoing particles with \(\mathbf{v}_3\) ad \(\mathbf{v}\). Since we are dealing with momentum conservation the inverse process is possible as well. * \(w(\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3,\mathbf{v}) f(\mathbf{x},\mathbf{v}_1,t) f(\mathbf{x},\mathbf{v}_2,t)\) is the rate at which the two colliding particles with \(\mathbf{v}_1\) and \(\mathbf{v}_2\) create density \(f(\mathbf{v})\) * \(-w(\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3,\mathbf{v})f(\mathbf{x},\mathbf{v}_3,t) f(\mathbf{x},\mathbf{v},t)\) is the rate at which \(f(\mathbf{v})\) is lost in a scattering to the benefit of densities \(f(\mathbf{v}_1)\) and \(f(\mathbf{v}_2)\) * Note that this process is a collision. It takes place at \(\mathbf{x}\), i.e. we assume point particles.
This process will drive the entire system into a global equilibrium. From a microscopic point of view it will drive the system locally at \(\mathbf{x}\). The collision term as given above is a nonlinear term in \(f\). We shall make use of a relaxation time approximation in our implementation of the discrete version of the BTE to read \[\left(\frac{\partial f(\mathbf{x},\mathbf{v})}{\partial t}\right)_{coll}=\frac{f^{eq}(\mathbf{x},\mathbf{v})-f(\mathbf{x},\mathbf{v})}{\tau}\] This means that the system is pushed towards an equilibrium distribution \(f^{eq}(\mathbf{x},\mathbf{v})\) with a rate \(\omega=1/\tau\). Note that this is a very simple model for the complicated microscopic scattering process. Nevertheless, taking into account that all transport processes occur on a much longer time scale this might be a good approximation, meaning that the external forces do not influence this process, i.e. they change on a much larger length scale than the interatomic ones.
The Lattice Boltzman method in two dimensions
The BTE is discretized in space, velocity and time. Discretizing Equation 3 on a regular (square) lattice in space is straightforward. However, we also require a suitable discretization of velocity space and the time step. Both are chosen such that the distance between interpolation points in velocity space multiplied by the time step equals the distance between points on the spatial lattice; in other words, a molecule traveling on the spatial lattice travels between integer number of lattice points during one time step.
The particular realization of the velocities used by us is shown in Figure 1. The velocity set contains 9 directions. Each direction is assigned the index shown in Figure 1. Direction \(0\) zero hence describes the population of molecules at rest. This specific discretization in two-dimensional space (\(D=2\)) with nine directions is commonly denoted by D2Q9.
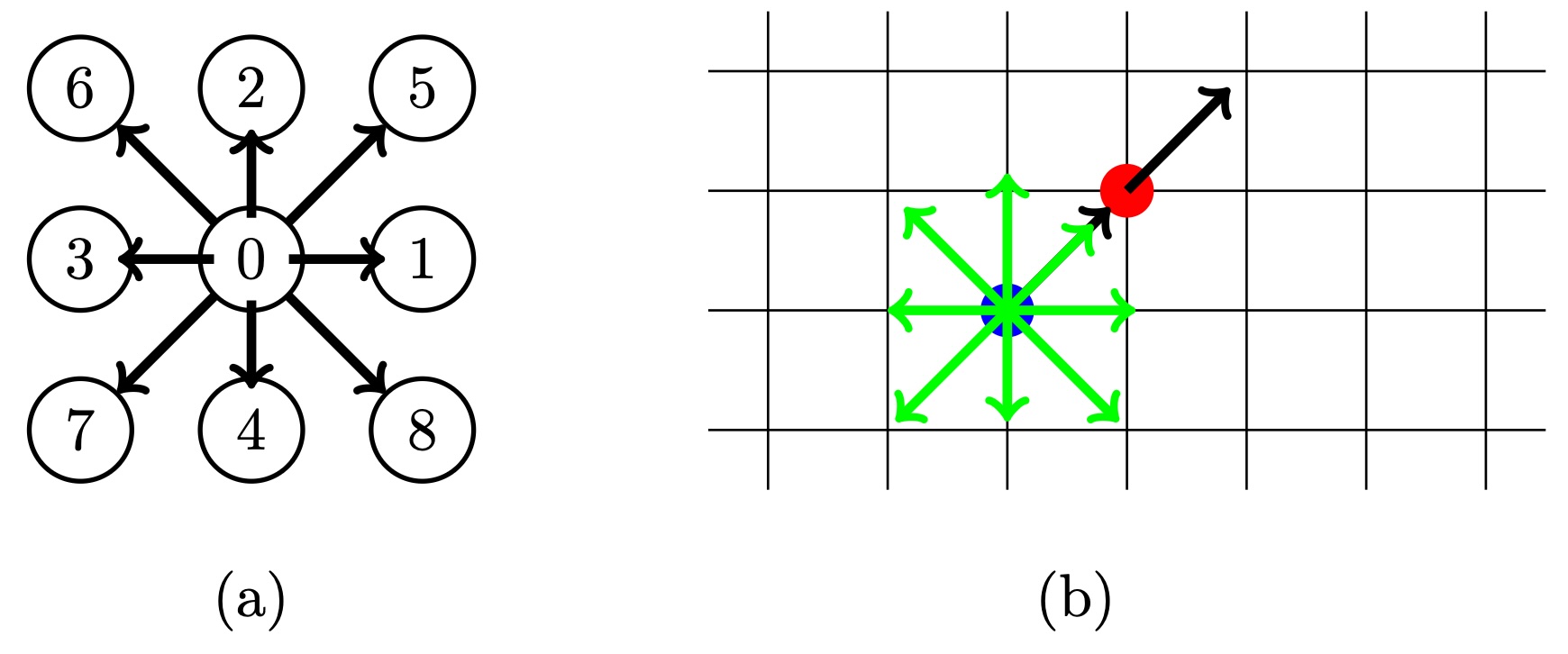
The discrete velocities are therefore given by the directions to the eight neighbors divided by the time step. We have nine velocity vectors \(\mathbf{c}_i\mbox{, with }i=0,\dots,8\) for each direction \(i\). We now also require the occupation numbers for these nine directions. The probability distribution \(f(\mathbf{r},\mathbf{v})\) is hence represented by nine discrete \(f_i(\mathbf{x}_j, t)\) where \(\mathbf{x}_j\) is the discrete lattice point \(i\) denotes the direction. Note that the moments of the probability density, Equation 1, become \[\begin{align} \rho(\mathbf{x}_j, t) &= \sum_i f_i(\mathbf{x}_j, t) \\ \mathbf{u}(\mathbf{x}_j, t) &= \frac{1}{ \rho(\mathbf{x}_j, t)} \sum_i \mathbf{c}_i f_i(\mathbf{x}_j, t), \end{align}\] where \(\rho(\mathbf{x}_j, t)\) is now the number density, i.e. we assume unit molecular mass.
The discretized BGK-Boltzmann equation (Equation 3) then reads \[ f_i(\mathbf{x}_j+\mathbf{c}_i\cdot\Delta t,t+\Delta t)=f_i(\mathbf{x}_j,t) -\omega[f_i(\mathbf{x}_j,t)-f_i^\text{eq}(\mathbf{x}_j,t)] \tag{4}\] where \(\Delta t\) is a time step used for the discrete dynamical propagation of the occupation numbers. We have introduced the normalized relaxation parameter \(\omega=\Delta t/\tau\) and the external forces \(\mathbf{F}(\mathbf{r})\) are set to zero. Note that the left hand side and the first term on the right hand side of Equation 4 is a discretization of the total differential of \(f\). The expression for the equilibrium distribution function in the nine directions is is (Mohamad 2011; Wolf-Gladrow 2000) \[ f_i^\text{eq}(\mathbf{x}_j, t) = w_i \rho(\mathbf{x}_j, t) 1 + 3 \mathbf{c}_i \cdot \mathbf{u}(\mathbf{x}_j, t) + \frac{9}{2} \left[\mathbf{c}_i \cdot \mathbf{u}(\mathbf{x}_j, t)\right]^2 - \frac{3}{2} u^2(\mathbf{x}_j, t), \tag{5}\] with \(w_i = 4/9\), \(1/9\) and \(1/36\) for directions \(0\), \(1\)-\(3\) and \(4\)-\(8\), respectively. Note that like Equation 2 for the continuous distribution function, Equation 5 is obtained by applying the maximum entropy principle under the constraint of mass and momentum conservation to the discrete distribution function (Mohamad 2011; Wolf-Gladrow 2000).
To give a rough idea of how Equation 4 propagates the occupation numbers for the individual directions, we describe as an example ppensto \(f_5\). Assume we have a finite value for direction \(f_i\) including \(f_5\), their magnitude given by the length of the green arrows, respectively, and based at the position shown by the blue spot in Figure 1. At time \(t\) the r.h.s. of Equation 4 relaxes \(f_5\) towards the local equilibrium given by the black arrow based at the blue spot, which is commonly called the collision operation (Boltzmann 1995). Time propagation is described by the l.h.s. of Equation 4. After one time step \(\Delta t\), the occupation \(f_5\) will be handed to the red spot and occupy direction \(5\) there. This is commonly called the streaming step. An algorithmic implementation of Equation 4 is conveniently split into these streaming and collision steps.
Watch the following video for a more thorough explanation.