Shear-wave decay

Shear Wave Decay

It is good practice to always validate the implementation of a numerical method with available analytical solutions. Among other a particularly effective method is to “measure” the viscosity of the simulated fluid and compare it to the one which was given as input (As done, for example, by Fei et al. for the cascaded lattice Boltzmann method [1]).

The shear wave decay represents the time evolution of a velocity perturbation in the flow which decreases to zero because of the effects of the viscosity. In order to obtain an analytical description of this phenomenon we consider the Navier-Stokes equations which are the continuum representation of the Lattice Boltzmann Equation:

\[\begin{equation} \begin{aligned} \nabla \cdot \mathbf{u} &= 0 \\ \dfrac{\partial \mathbf{u}}{\partial t} + \left( \mathbf{u} \cdot \nabla \right) \mathbf{u} + \dfrac{1}{\rho} \nabla p &= \nu \nabla^2 \mathbf{u} \end{aligned} \label{eq:NS_def}\tag{1} \end{equation}\]

where \(\nu\) is the kinematic viscosity. The system of equations \(\ref{eq:NS_def}\) is completed by the following boundary and initial conditions:

\[\begin{equation} \begin{aligned} &\mathbf{u}(x,y,z,0) = \mathbf{u}_0 \,\,\,\, \text{initial condition} \\ &\mathbf{u}(x,y,z,t)|_{S} = \bar{\mathbf{u}}(x,y,z,t) \,\,\,\, \text{boundary condition} \end{aligned} \end{equation}\]

Since no analytical solution is available for the 3D case, we have to make the following assumptions: 1. We consider a small velocity perturbation so that the velocity gradient is small enough to neglect the nonlinear term (\(\mathbf{u} \cdot \nabla ) \mathbf{u}\) in Eq. \(\ref{eq:NS_def}\). 2. The pressure gradient \(\nabla p\) is also small and negligible.

Therefore we can express the momentum balance in equation \(\ref{eq:NS_def}\) as:

\[\begin{equation} \dfrac{\partial \mathbf{u}}{\partial t} = \nu \nabla^2 \mathbf{u} \label{eq:mom_simplified}\tag{2} \end{equation}\]

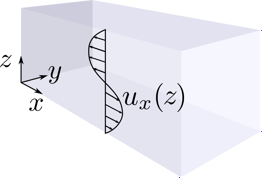Figure 1: One dimensional velocity perturbation in a 3D periodic domain.

Now we consider a periodic 3D domain with dimensions \(L_x\), \(L_y\) and \(L_z\) as shown in figure 1. We introduce a sinusoidal perturbation in the velocity component in the \(x\)-direction:

\[\begin{equation} \mathbf{u}(\mathbf{x},t=0) = \begin{pmatrix} u_x(z) \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} a_0 \sin \dfrac{2 \pi}{L_z} z \\ 0 \\ 0 \end{pmatrix} \end{equation}\]

where \(a_0\) is the initial perturbation amplitude which is chose small enough in order to satisfy the assumptions.

Since equation \(\ref{eq:mom_simplified}\) is a linear partial differential equation, we know that the solution to a periodic perturbation will be of the form:

\[\begin{equation} u_x(z,t) = a(t) \phi(z). \label{eq:u_decomp}\tag{3} \end{equation}\]

Moreover, only the perturbation in the \(x\)-direction is relevant, hence we can consider only this component of equation \(\ref{eq:mom_simplified}\):

\[\begin{equation} \dfrac{\partial u_x(z,t)}{\partial t} = \nu \dfrac{\partial^2}{\partial z^2} u_x (z,t). \label{eq:1D_stokes}\tag{4} \end{equation}\]

By substituting Eq.\(\ref{eq:u_decomp}\) into the \(\ref{eq:1D_stokes}\) we can differentiate the sinusoidal component in space:

\[\begin{equation} \dfrac{\partial a(t)}{\partial t} \phi(z) = \nu a(t) \phi^{\prime \prime} (z). \label{eq:1D_stokes2}\tag{5} \end{equation}\] \[\begin{equation} \dfrac{\partial a(t)}{\partial t} \sin \left( \dfrac{2 \pi}{L_z} z \right) = - \nu \left( \dfrac{2 \pi}{L_z} \right)^2 a(t) \sin \left( \dfrac{2 \pi}{L_x} z \right). \label{eq:1D_stokes3}\tag{6} \end{equation}\]

The two sinusoidal parts in equation \(\ref{eq:1D_stokes3}\) cancel each other. Therefore one obtains an ordinary differential equation which describes the time evolution of the amplitude of the perturbation:

\[\begin{equation} \dfrac{da(t)}{dt} = -\nu \zeta^2 a(t) \label{eq:exp_1d}\tag{7} \end{equation}\]

with \(\zeta=\frac{2 \pi}{L_z}\). The solution equation \(\ref{eq:exp_1d}\) is given by:

\[\begin{equation} a(t) = a_0 e^{-\nu\zeta^2 t} = a_0 e^{-\nu(\frac{2 \pi}{L_z})^2 t}. \label{eq:amp_solution}\tag{8} \end{equation}\]

This means that the velocity field will evolve in time with an exponential decay while the shape of perturbation in space will remain sinusoidal:

\[\begin{equation} \mathbf{u}(\mathbf{x},t) = \begin{pmatrix} u_x(z,t) \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} a_0 e^{-\nu(\frac{2 \pi}{L_z})^2 t} \sin \dfrac{2 \pi}{L_z} z \\ 0 \\ 0 \end{pmatrix} \end{equation}\]

Equation 8 represents the analytical time evolution of the perturbation amplitude. This analytical result can be compared with the measured decay of the perturbation \(a_{sim}(t)\) out of the simulation results. If \(a_{sim}(t) = a(t)\) the simulated fluid has the same viscosity as expected from the input parameters \(\nu\).

Video

References

[1] L. Fei, K. H. Luo, and Q. Li. Three-dimensional cascaded lattice boltzmann method:Improved implementation and consistent forcing scheme.Physical Review E, 97(5):053309, 2018.