Chapter 10
Data structures & implementation
Context: In this chapter, we will show how a simple finite element solver can be implemented in the Python programming language using our example of solving the Poisson equation. Here, we assume that the charge density vanishes. Thus, we calculate the spatial distribution of the electrostatic potential under appropriate boundary conditions. We will use this to calculate the capacitance of a plate capacitor.
10.1 Example problem
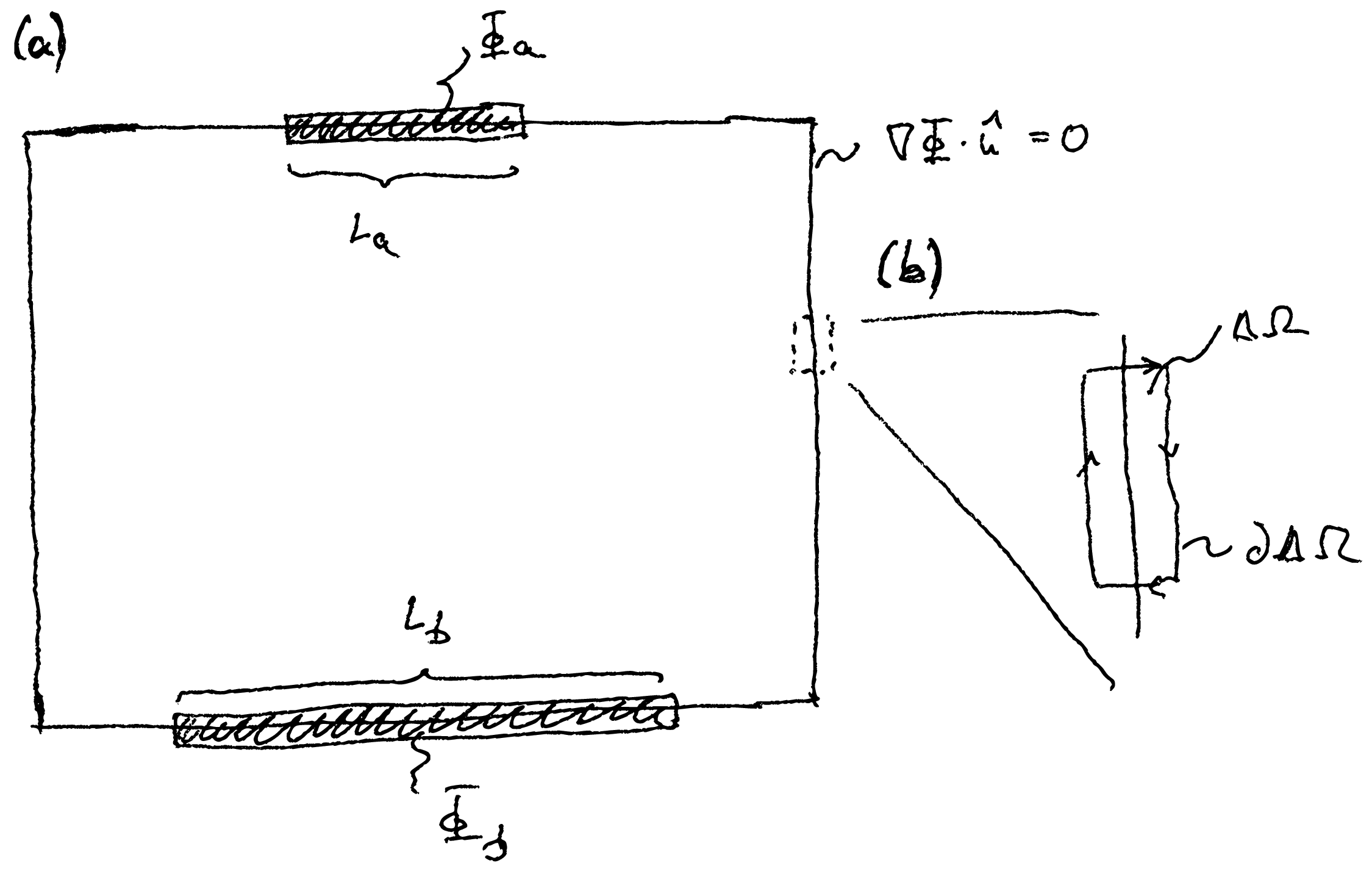
We will now further develop our example problem from the previous chapter and calculate the capacitance of a plate capacitor. To do this, we assume an infinitesimal charge density in the capacitor, \(\rho =0\). The Poisson equation then becomes the Laplace equation, \begin {equation} \nabla ^2 \Phi = 0. \end {equation} The plates of the capacitor are assumed to be metallic, i.e. the potential on the capacitor plates is constant (see Fig. 10.1a). This is modeled by a Dirichlet boundary condition. The rest of the domain is given a Neumann boundary condition, in which the derivative on the surface disappears.
In the context of the Poisson or Laplace equation, directional derivatives at the boundary have a simple interpretation. We look at a small volume element \(\Delta \Omega \) at the boundary of the area (see Fig. 10.1b). Integrating the Poisson equation over this area yields, \begin {equation} \int _{\Delta \Omega }\dif ^3 r\, \nabla ^2 \Phi = \int _{\partial \Delta \Omega }\dif ^2 r\, \nabla \Phi \cdot \hat {n}(\v {r}) = \frac {1}{\varepsilon } \int _{\Delta \Omega }\dif ^3 r\, \rho (\v {r}), \end {equation} where the integration over \(\partial \Delta \Omega \) is done along the path shown in Fig. Now, we assume that the two sides of the path that are perpendicular to the boundary of the domain are negligible compared to the other two sides. Furthermore, we assume that only a surface charge \(\sigma (\v {r})\) lives in the domain. This yields \begin {equation} \int _{\partial \Delta \Omega }\dif ^2 r \ \hat {n}(\v {r}) \cdot \nabla \Phi = \frac {1}{\varepsilon } \int _{\Delta A} \dif ^2 r \ \sigma (\v {r}), \end {equation} where \(\Delta A\) is the area of the boundary of the simulation domain that lies within \(\Delta \Omega \). Assuming that the space outside the simulation domain is field-free, i.e. \(\nabla \Phi =0\), then \begin {equation} \nabla \Phi \cdot \hat {n}(\v {r}) = \frac {\sigma (\v {r})}{\varepsilon }, \label {eq:surfacecharge} \end {equation} the directional derivative thus yields the surface charge at the boundary.
The absence of a field outside our simulation domain is only exactly fulfilled at the electrodes. These are metallic and therefore by definition free of fields. (A field inside an ideal metal immediately leads to a rearrangement of charges that then compensate for this field). This means that we can use Eq. \eqref{eq:surfacecharge} to calculate the charge induced on the capacitor plates. Together with the potential given by the Dirichlet boundary conditions, this can be used to calculate the capacitance on the capacitor plates.
On the other hand, the implicit Neumann boundary condition \(\nabla \Phi \cdot \hat {n}=0\) means that our simulation is carried out under conditions in which the boundary is charge-free but outside the simulation domain the field disappears. This is an artificial condition that can cause errors. So you have to make sure that the simulation domain is large enough in the direction parallel to the capacitor plates to properly capture the stray fields at the edge of the capacitor.
10.2 Data Structures
The central data structure for numerical applications is the multidimensional array, numpy.ndarray, of the numpy library. Multidimensional arrays reserve memory for a certain number of entries. (These entries are also called elements, but in order to avoid confusion with finite elements, they will be referred to throughout this document as entries.) An array of length \(10\) filled with zeros (i.e. \(10\) entries) is obtained by
1import numpy as np 2a = np.zeros(10)
This array has the dimension \(1\). The multidimensional character of the arrays manifests itself in the fact that the arrays implicitly implement a mapping of several coordinates to a linear index. A two-dimensional array can be obtained, for example, by
1b = np.zeros([2, 5])
You can now access the array entries, e.g.
1a[6] 2b[1, 1]
Both commands access entry \(6\) of the underlying memory area. A natural use of multidimensional arrays is the representation of vectors (\(1\)-dimensional arrays) or matrices (\(2\)-dimensional arrays).
However, we will use these properties in the optimized, vectorized implementation of the example problem in these chapters to map the structure of our grid.
Note: The statement that
1a[6] 2b[1, 1]
accesses the same entry of the underlying memory area in the above example depends on the storage order. It is only true if the last index is stored compactly in memory. This storage order is called “row major” because in a two-dimensional array, i.e. a matrix, the rows are stored compactly in memory. If the first index is the compact one, it is called “column major”. In numpy, “row major” is also called “C-continguous” and “column major” is called “F-contiguous”. This is because in the C programming language the memory order is “row major” and in the Fortran programming language the memory order is “column major”. Arrays in numpy are “column major” by default, but other memory orders are supported and do occur.
10.3 Initialization
The example implementations follow simple rules for readable computer code. This should always be written in a way that a third person can read and reuse it. We will therefore...
- ...use only English language.
- ...write out variable names and do not use symbols as variable names (e.g.
potentialand not the written out symbolphias the name). - ...add a suffix to array variables that indicates the type of indices (e.g.
potential_xyto indicate that there are two indices corresponding to the positions \(x\) and \(y\)). - ...document the code with comment blocks and Python docstrings. We recommend the numpydoc standard for docstrings.
In this implementation, we use explicit loops to improve the readability of the code. The code can still be vectorized by using numpy operations.
First, we have to initialize the code and determine how many grid points we want to use. We define the variables
1# Grid size, number of nodes 2nb_nodes = 32, 32 3Nx, Ny = nb_nodes
We now also determine the range over which the two electrodes of the capacitor should extend:
1# Top capacitor plate 2top_left = Nx//4 3top_right = 3*Nx//4-1 4top_potential = 1 5 6# Bottom capacitor plate 7bottom_left = Nx//4 8bottom_right = 3*Nx//4-1 9bottom_potential = -1
The area is specified here with node indices. Furthermore, we still need the element matrix that we store in a numpy.ndarray:
1# Element matrix, index l indicates element-local node 2element_matrix_ll = np.array([[1, -1/2, -1/2], 3[-1/2, 1/2, 0], 4[-1/2, 0, 1/2]])
The suffix _ll indicates that there are two indices (the array is two-dimensional), both of which denote a local element node. We then initialize the system matrix and the right-hand side, initially with zeros:
1# System matrix, index g indicates global node 2system_matrix_gg = np.zeros([Nx*Ny, Nx*Ny]) 3 4# Right hand side 5rhs_g = np.zeros(Nx*Ny)
The suffix _g denotes the index of the global node. The variable rhs_g contains the vector \(\v {f}\) and therefore needs only one index. The variable system_matrix_gg contains the system matrix \(\t {K}\) and therefore needs two global node indices.
10.4 System matrix
The core of the simulation program is the structure of the system matrix. In this section, this is realized by explicit loops. The next section shows how this can be done in a more compact (and efficient) but less transparent way using special numpy commands.
First, we define a function that turns node coordinates into the global node index:
1def node_index(i, j, nb_nodes): 2 """ 3 Turn node coordinates (i, j) into their global node index. 4 5 Parameters 6 ---------- 7 i : int 8 x-coordinate (integer) of the node 9 j : int 10 y-coordinate (integer) of the node 11 nb_nodes : tuple of ints 12 Number of nodes in the Cartesian directions 13 14 Returns 15 ------- 16 g : int 17 Global node index 18 """ 19 Nx, Ny = nb_nodes 20 return i + Nx*j
We use this in another auxiliary function that adds the element matrix to the system matrix. To do this, the element matrix must first be stretched to the system matrix. The function looks like this:
1def add_element_matrix(system_matrix_gg, element_matrix_ll, 2 global_node_indices): 3 """ 4 Add element matrix to global system matrix. 5 6 Parameters 7 ---------- 8 system_matrix_gg : array_like 9 N x N system matrix where N is the number of global 10 nodes. This matrix will be modified by this function. 11 element_matrix_ll : array_like 12 n x n element matrix where n is the number of local 13 nodes 14 global_node_indices : list of int 15 List of length n that contains the global node 16 indices for the local node index that corresponds to 17 the list position. 18 """ 19 assert element_matrix_ll.shape == \ 20 (len(global_node_indices), len(global_node_indices)) 21 for i in range(len(global_node_indices)): 22 for j in range(len(global_node_indices)): 23 system_matrix_gg[global_node_indices[i], 24 global_node_indices[j]] += \ 25 element_matrix_ll[i, j]
The assert statement is a watchdog here, making sure that the local element matrix and the global_node_indices array have the same length. The two for loops then run through all the entries in the element matrix. The expression global_node_indices[i] then returns the global node index that corresponds to the local node index of the element matrix. The system matrix is then assembled by calling this auxiliary method for each element:
1def assemble_system_matrix(element_matrix_ll, nb_nodes): 2 """ 3 Assemble system matrix from the element matrix 4 5 Parameters 6 ---------- 7 element_matrix_ll : array_like 8 3 x 3 element matrix 9 nb_nodes : tuple of ints 10 Number of nodes in the Cartesian directions 11 12 Returns 13 ------- 14 system_matrix_gg : numpy.ndarray 15 System matrix 16 """ 17 18 Nx, Ny = nb_nodes 19 Mx, My = Nx-1, Ny-1 # number of boxes 20 21 # System matrix 22 system_matrix_gg = np.zeros([Nx*Ny, Nx*Ny]) 23 24 # Construct system matrix 25 for l in range(Mx): 26 for m in range(My): 27 # Element (0) 28 n0 = node_index(l, m, nb_nodes) 29 n1 = node_index(l+1, m, nb_nodes) 30 n2 = node_index(l, m+1, nb_nodes) 31 add_element_matrix(system_matrix_gg, 32 element_matrix_ll, 33 [n0, n1, n2]) 34 35 # Element (1) 36 n0 = node_index(l+1, m+1, nb_nodes) 37 n1 = node_index(l, m+1, nb_nodes) 38 n2 = node_index(l+1, m, nb_nodes) 39 add_element_matrix(system_matrix_gg, 40 element_matrix_ll, 41 [n0, n1, n2]) 42 43 return system_matrix_gg
Here, the two for loops run over the individual boxes. The loop over the two elements per box is explicitly written as two calls to add_element_matrix. The variables n0, n1 and n2 contain the global node indices describing the corners of the respective element.
The system matrix that has now been constructed has (implicitly) Neumann boundary conditions with \(\nabla \Phi \cdot \hat {n}(\v {r})=0\) on the boundary. We now have to add the Dirichlet conditions for the electrodes. To do this, we replace the rows of the system matrix and the corresponding entries of the load vector:
1def capacitor_bc(system_matrix_gg, rhs_g, 2 top_left, top_right, top_potential, 3 bottom_left, bottom_right, bottom_potential, 4 nb_nodes): 5 """ 6 Set boundary conditions for the parallel plate capacitor. 7 8 Parameters 9 ---------- 10 system_matrix_gg : numpy.ndarray 11 System matrix. The system matrix is modified by a call 12 to this function 13 rhs_g : numpy.ndarray 14 Right-hand side vector. The right-hand side vector is 15 modified by a call to this function. 16 top_left : int 17 Leftmost node of the top electrode 18 top_right : int 19 Rightmost node of the top electrode 20 top_potential : float 21 Electrostatic potential of the top electrode 22 bottom_left : int 23 Leftmost node of the bottom electrode 24 bottom_right : int 25 Rightmost node of the bottom electrode 26 bottom_potential : float 27 Electrostatic potential of the bottom electrode 28 nb_nodes : tuple of ints 29 Number of nodes in the Cartesian directions 30 """ 31 Nx, Ny = nb_nodes 32 # Dirichlet boundary conditions for top plate 33 for i in range(top_left, top_right+1): 34 n = node_index(i, Ny-1, nb_nodes) 35 mat_g = np.zeros(Nx*Ny) 36 mat_g[n] = 1 37 system_matrix_gg[n] = mat_g 38 rhs_g[n] = top_potential 39 40 # Dirichlet boundary conditions for bottom plate 41 for i in range(bottom_left, bottom_right+1): 42 n = node_index(i, 0, nb_nodes) 43 mat_g = np.zeros(Nx*Ny) 44 mat_g[n] = 1 45 system_matrix_gg[n] = mat_g 46 rhs_g[n] = bottom_potential
The entire simulation code now contains calls to these functions, followed by the numerical solution of the linear system of equations:
1# Construct system matrix 2system_matrix_gg = assemble_system_matrix(element_matrix_ll, 3 nb_nodes) 4 5# Boundary conditions 6capacitor_bc(system_matrix_gg, rhs_g, 7 top_left, top_right, top_potential, 8 bottom_left, bottom_right, bottom_potential, 9 nb_nodes) 10 11# Solve system of linear equations 12potential_g = np.linalg.solve(system_matrix_gg, rhs_g)
The variable potential_g now contains the values of the electrostatic potential on the nodes.
10.5 Visualization
The result of the calculation can be visualized using the matplotlib library. The function matplotlib.pyplot.tripcolor can plot data on a triangulated 2D grid. The following code block visualizes the result of the simulation using this function.
1import matplotlib.pyplot as plt 2import matplotlib.tri 3 4def make_grid(nb_nodes): 5 """ 6 Make an array that contains all elements of the grid. The 7 elements are described by the global node indices of 8 their corners. The order of the corners is in order of 9 the local node index. 10 11 They are sorted in geometric positive order and the first 12 is the node with the right angle corner at the bottom 13 left. Elements within the same box are consecutive. 14 15 This is the first element per box: 16 17 2 18 | \ 19 | \ 20 dy | \ 21 | \ 22 0 --- 1 23 24 dx 25 26 This is the second element per box: 27 28 dx 29 1 ---0 30 \ | 31 \ | dy 32 \ | 33 \| 34 2 35 36 Parameters 37 ---------- 38 nb_nodes : tuple of ints 39 Number of nodes in the Cartesian directions 40 41 Returns 42 ------- 43 triangles_el : numpy.ndarray 44 Array containing the global node indices of the 45 element corners. The first index (suffix _e) 46 identifies the element number and the second index 47 (suffix _l) the local node index of that element. 48 """ 49 Nx, Ny = nb_nodes 50 # These are the node position on a subsection of the grid 51 # that excludes the rightmost and topmost nodes. The 52 # suffix _G indicates this subgrid. 53 y_G, x_G = np.mgrid[:Ny-1, :Nx-1] 54 x_G.shape = (-1,) 55 y_G.shape = (-1,) 56 57 # List of triangles 58 lower_triangles = np.vstack( 59 (node_index(x_G, y_G, nb_nodes), 60 node_index(x_G+1, y_G, nb_nodes), 61 node_index(x_G, y_G+1, nb_nodes))) 62 upper_triangles = np.vstack( 63 (node_index(x_G+1, y_G+1, nb_nodes), 64 node_index(x_G, y_G+1, nb_nodes), 65 node_index(x_G+1, y_G, nb_nodes))) 66 # Suffix _e indicates global element index 67 return np.vstack( 68 (lower_triangles, upper_triangles)).T.reshape(-1, 3) 69 70def plot_results(values_g, nb_nodes, mesh_style=None, 71 ax=None): 72 """ 73 Plot results of a finite-element calculation on a 74 two-dimensional structured grid using matplotlib. 75 76 Parameters 77 ---------- 78 nb_nodes : tuple of ints 79 Number of nodes in the Cartesian directions 80 values_g : array_like 81 Expansion coefficients (values of the field) on the 82 global nodes 83 mesh_style : str, optional 84 Will show the underlying finite-element mesh with 85 the given style if set, e.g. ’ko-’ to see edges 86 and mark nodes by points 87 (Default: None) 88 ax : matplotlib.Axes, optional 89 Axes object for plotting 90 (Default: None) 91 92 Returns 93 ------- 94 trim : matplotlib.collections.Trimesh 95 Result of tripcolor 96 """ 97 Nx, Ny = nb_nodes 98 99 # These are the node positions on the full global grid. 100 y_g, x_g = np.mgrid[:Ny, :Nx] 101 x_g.shape = (-1,) 102 y_g.shape = (-1,) 103 104 # Gouraud shading linearly interpolates the color between 105 # the nodes 106 if ax is None: 107 ax = plt 108 triangulation = matplotlib.tri.Triangulation( 109 x_g, y_g, make_grid(nb_nodes)) 110 c = ax.tripcolor(triangulation, values_g, 111 shading=’gouraud’) 112 if mesh_style is not None: 113 ax.triplot(triangulation, mesh_style) 114 return c 115 116 plt.subplot(111, aspect=1) 117 plot_results(potential_g, nb_nodes, show_mesh=True) 118 plt.xlabel(r’$x$-position ($\Delta x$)’) 119 plt.ylabel(r’$y$-position ($\Delta y$)’) 120 plt.colorbar().set_label(r’Potential $\Phi$ (V)’) 121 plt.tight_layout() 122 plt.show()
The make_grid function here generates a list of global node indices per element. The first index is the index of the element (suffix e), the second index is the local node index within the element (suffix l). The nodes of the respective element are numbered counterclockwise. For visualization, “Gouraud” shading is used. This type of coloring linearly interpolates the value of the nodes on the triangles and exactly matches the interpolation rule of our shape functions. We can thus represent the full interpolated function \(\Phi _N(\v {r})\).
10.6 Example: Plate capacitor
With the help of the code developed here, the electrostatic potential within a plate capacitor can now be calculated. Figure 10.2 shows the result of this calculation for different resolutions of the simulation, i.e. different numbers of elements. By increasing the resolution, the simulation can be systematically improved.
To calculate the capacitance, we now have to determine the charge on the capacitor plates. The total charge \(Q_\alpha \) on the electrode \(\alpha \) is obtained from the surface charge given by Eq. \eqref{eq:surfacecharge}. By integrating over the area of the capacitor plates \(A_\alpha \), we obtain \begin {equation} Q_\alpha = \int _{A_\alpha } \dif ^2 r\, \sigma (\v {r}) = \varepsilon \int _{A_\alpha } \dif ^2 r\, \nabla \Phi _N\cdot \hat {n}(\v {r}). \end {equation} Here, the permittivity \(\varepsilon \) plays an important role for the unit of the charge. We can now use the series expansion again. Only element type \((1)\) contributes to the integral, and here only the shape functions for which the derivative in the \(y\) direction does not vanish, since \(\nabla \Phi _N\cdot \hat {n}(\v {r})=\pm \partial \Phi _N/\partial y\). The sign is reversed for the upper and lower capacitor plates. Non-vanishing contributions come from the form functions \(N_0^{(1)}\) and \(N_2^{(1)}\). We get \begin {align} \int _0^{\Delta x} \dif x \frac {\partial N_0^{(1)}}{\partial y} &= \int _0^{\Delta x} \dif x \frac {1}{\Delta y} = \frac {\Delta x}{\Delta y} \\ \int _0^{\Delta x} \dif x \frac {\partial N_2^{(1)}}{\partial y} &= \int _0^{\Delta x} \dif x \left (-\frac {1}{\Delta y}\right ) = -\frac {\Delta x}{\Delta y} \end {align}
and thus for \(\Delta x=\Delta y\) \begin {equation} Q^{(n)} = \varepsilon t(a_0 - a_2) \end {equation} as the contribution of the element \((n)\) to the charge on the electrode. Here, the indices of the coefficients \(a_0\) and \(a_2\) denote the respective local node indices. The quantity \(t\) is the depth of the simulation domain. Since we are considering the problem here in two dimensions, all charges are effectively line charges (per depth) and the factor \(t\) is needed to obtain an absolute charge. Our plate capacitor is infinitely long in the third dimension. The factor \(\varepsilon t\) has the unit farad and is therefore a capacitance.
The capacitance of the capacitor is now given by \(C=Q_0/\Delta \Phi \), where \(Q_0\) is the charge on one capacitor plate and \(\Delta \Phi \) is the (given) potential difference. The second capacitor plate must carry the charge \(Q_1=-Q_0\). The code for calculating the charge on the capacitor plates therefore looks like this:
1def get_charge(potential_g, nb_nodes, 2top_left, top_right, 3 bottom_left, bottom_right): 4 """ 5 Compute charge on both capacitor plates. 6 7 Parameters 8 ---------- 9 potential_g : array_like 10 Electrostatic potential 11 nb_nodes : tuple of ints 12 Number of nodes in the Cartesian directions 13 top_left : int 14 Leftmost node of the top electrode 15 top_right : int 16 Rightmost node of the top electrode 17 bottom_left : int 18 Leftmost node of the bottom electrode 19 bottom_right : int 20 Rightmost node of the bottom electrode 21 22 Returns 23 ------- 24 charge_top : float 25 Charge (divided by permittivity and thickness) on top 26 plate 27 charge_bottom : float 28 Charge (divided by permittivity and thickness) on 29 bottom plate 30 """ 31 Nx, Ny = nb_nodes 32 charge_top = 0.0 33 for i in range(top_left+1, top_right+1): 34 charge_top += \ 35 potential_g[node_index(i, Ny-1, nb_nodes)] - \ 36 potential_g[node_index(i, Ny-2, nb_nodes)] 37 38 charge_bottom = 0.0 39 for i in range(bottom_left+1, bottom_right+1): 40 charge_bottom += \ 41 potential_g[node_index(i, 0, nb_nodes)] - \ 42 potential_g[node_index(i, 1, nb_nodes)] 43 44 return charge_top, charge_bottom
Of course, we know what the capacitance of a plate capacitor looks like. It is given by \begin {equation} C = \varepsilon \frac {A}{d}, \label {eq:anacapacity} \end {equation} where \(A=tL\) is the area of the capacitor plate and \(d\) is the distance between the plates. (\(L\) is the length of the plates, see Fig. 10.1a.) We can write this in dimensionless form as \begin {equation} \frac {C}{\varepsilon t} = \frac {L}{d}. \end {equation} We get the left side directly from our simulation. The result of the finite element calculation is shown in Fig. 10.3 compared with this analytical expression. You can see that the analytical expression only applies to small aspect ratios \(d/L<1\). The derivation of this expression assumes that the field lines are everywhere parallel and perpendicular to the capacitor plates. For large distances between the capacitor plates, this is no longer the case and stray fields at the edge of the plates begin to play a role in the capacitance. These are not included in Eq. \eqref{eq:anacapacity}, but are modeled in the simulation.
Note: The system matrix of the finite element method is sparse. For sparse matrices, there are special data structures that simplify the handling of these matrices. These are implemented in the scipy.sparse package. We can use these routines to construct a sparse system matrix:
1from scipy.sparse import coo_matrix 2 3def assemble_system_matrix(element_matrix_ll, nb_nodes): 4 """ 5 Assemble system matrix from the element matrix 6 7 Parameters 8 ---------- 9 element_matrix_ll : array_like 10 3 x 3 element matrix 11 nb_nodes : tuple of ints 12 Number of nodes in the Cartesian directions 13 14 Returns 15 ------- 16 system_matrix_gg : numpy.ndarray 17 System matrix 18 """ 19 Nx, Ny = nb_nodes 20 21 # Compute grid 22 grid_el = make_grid(nb_nodes) 23 24 # Get number of elements 25 nb_elements, nb_corners = grid_el.shape 26 27 # Spread out grid and element matrix such that they can 28 # be used as global node coordinates for the sparse 29 # matrix 30 grid1_ell = np.stack( 31 [grid_el, grid_el, grid_el], axis=1) 32 grid2_ell = np.stack( 33 [grid_el, grid_el, grid_el], axis=2) 34 element_matrix_ell = np.stack( 35 [element_matrix_ll]*nb_elements, axis=0) 36 37 # Construct sparse system matrix 38 # ‘coo_matrix‘ will automatically sum duplicate entries 39 system_matrix_gg = coo_matrix( 40 (element_matrix_ell.reshape(-1), 41 (grid1_ell.reshape(-1), grid2_ell.reshape(-1))), 42 shape=(Nx*Ny, Nx*Ny)) 43 44 return system_matrix_gg.todense()
This method replaces the above implementation of assemble_system_matrix. For reasons of compatibility with the rest of the implementation shown here, it returns a dense matrix at the end, but you can continue to work with the sparse matrix. As part of the application of coo_matrix, the global node indices are used here as the “coordinates” of the matrix entries. To do this, both the node indices and the entries of the element matrix must be multiplied by the size of the system matrix. This is done by the numpy.stack commands in these code fragments.