Chapter 5
Numerical solution
Context: We will now put the transport problem aside for a while and devote ourselves to the numerical solution of differential equations. This chapter illustrates the basic ideas behind numerical analysis of differential equations. It introduces a few important concepts, in particular the series expansion and the residual. The presentation here follows chapter 1 from Boyd (2000).
5.1 Series expansion
In abstract notation, we are looking for unknown functions \(u(x,y,z,...)\) that solve a set of differential equations \begin {equation} \mathcal {L} u(x,y,z,\ldots ) = f(x,y,z,\ldots ) \label {eq:gendgl} \end {equation} must be fulfilled. Here, \(\mathcal {L}\) is a (not necessarily linear) operator that contains the differential (or integral) operations. We now introduce an important concept for the (numerical) solution of the differential equation: We approximate the function \(u\) by a truncated series expansion of \(N\) terms. We write \begin {equation} u_N(x, y, z, \ldots ) = \sum _{n=1}^N a_n \varphi _n(x,y,z,\ldots ) \label {eq:seriesexpansion} \end {equation} where the \(\varphi _n\) are called “basis functions”. We will discuss the properties of these basis functions in more detail in the next chapter.
We can now write the differential equation as, \begin {equation} \mathcal {L} u_N(x,y,z,\ldots ) = f(x,y,z,\ldots ). \end {equation} This representation means that we have now replaced the question of the unknown function \(u\) with the question of the unknown coefficients \(a_n\). We only have to let the differential operator \(\mathcal {L}\) act on the (known) basis functions \(\varphi _n\) and we can calculate this analytically.
What remains is to determine the coefficients \(a_n\). These coefficients are numbers, and these numbers can be calculated by a computer. Equation \eqref{eq:seriesexpansion} is of course an approximation. For certain basis functions, it can be shown that these are “complete” and can therefore represent certain classes of functions exactly. However, this is only true under the condition that the series Eq. \eqref{eq:seriesexpansion} is extended to \(N\to \infty \). For all practical applications (such as implementations in computer code), however, this series expansion must be aborted. A “good” series expansion approximates the exact solution already at low \(N\) with a small error. With this statement, we would of course have to specify how we want to quantify errors. Numerically, we then search for the exact coefficients \(a_n\) that minimize the error. The choice of a good basis function is non-trivial.
5.2 Residual
An important concept is that of the residual. Our goal is to solve Eq. \eqref{eq:gendgl}. The exact solution would be \(\mathcal {L} u - f\equiv 0\). However, since we can only construct an approximate solution, this condition will not be fulfilled exactly. We define the residual as exactly this deviation from the exact solution, namely \begin {equation} R(x,y,z,\ldots ; a_0, a_1, \ldots , a_N) = \mathcal {L} u_N(x,y,z,\ldots ) - f(x,y,z,\ldots ). \label {eq:residual} \end {equation} The residual is therefore a kind of measure for the error we make. The strategy for numerically solving the differential equation Eq. \eqref{eq:gendgl} is now to determine the coefficients \(a_n\) in such a way that the residual Eq. \eqref{eq:residual} is minimal. We have thus mapped the solution of the differential equation to an optimization problem. The different numerical methods, which we will discuss in the next chapters, are mainly determined by the specific optimization strategy.
Note: Numerical methods for optimization are a central core of the numerical solution of differential equations and thus of simulation techniques. There are countless optimization methods that work better or worse in different situations. We will first treat such optimizers as “black boxes”. At the end of the course, we will return to the question of optimization and discuss some well-known optimization methods. The term minimization method is often used synonymously with optimization methods. A good overview of optimization methods can be found in the book by Nocedal and Wright (2006).
5.3 A first example
We now want to concretize these abstract ideas using an example and introduce a few important terms. Let’s look at the one-dimensional boundary value problem, \begin {equation} \frac {\dif ^2 u}{\dif x^2} - (x^6 + 3x^2)u = 0, \label {eq:odeexample} \end {equation} with the boundary conditions \(u(-1)=u(1)=1\). (I.e. \(x\in [-1,1]\) is the domain on which we are looking for the solution.) In this case, the abstract differential operator \(\mathcal {L}\) takes the concrete form \begin {equation} \mathcal {L} = \frac {\dif ^2 }{\dif x^2} - (x^6 + 3x^2) \end {equation} is given. The exact solution to this problem is given by \begin {equation} u(x) = \exp \left [(x^4-1)/4\right ]. \end {equation}
We now guess an approximate solution as a series expansion for this equation. This approximate solution should already fulfill the boundary conditions. The equation \begin {equation} u_2(x) = 1 + (1-x^2)(a_0 + a_1 x + a_2 x^2) \label {eq:approxexample} \end {equation} is constructed in such a way that the boundary conditions are fulfilled. We can express these as \begin {equation} u_2(x) = 1 + a_0 (1-x^2) + a_1 x (1-x^2) + a_2 x^2 (1-x^2) \end {equation} to exponentiate the basis functions \(\varphi _i(x)\). Here \(\varphi _0(x)=1-x^2\), \(\varphi _1(x)= x (1-x^2)\) and \(\varphi _2(x) = x^2 (1-x^2)\). Since these basis functions are non-zero on the entire domain \([-1,1]\), this basis is called a spectral basis. (Mathematically: The carrier of the function corresponds to the domain.)
In the next step, we must find the residual \begin {equation} R(x; a_0, a_1, a_2) = \frac {\dif ^2 u_2}{\dif x^2} - (x^6 + 3x^2)u_2 \end {equation} minimize. For this we choose a strategy called collocation: We require that the residual vanishes exactly at three selected points: \begin {equation} R(x_i; a_0, a_1, a_2)=0 \quad \text {for}\quad x_0=-1/2, x_1=0\;\text {und}\;x_2=1/2. \end {equation}
Note: The disappearance of the residual at \(x_i\) does not mean that \(u_2(x_i)\equiv u(x_i)\), i.e. that at \(x_i\) our approximate solution corresponds to the exact solution. We are still restricted to a limited set of functions, namely the functions covered by Eq. \eqref{eq:approxexample}.
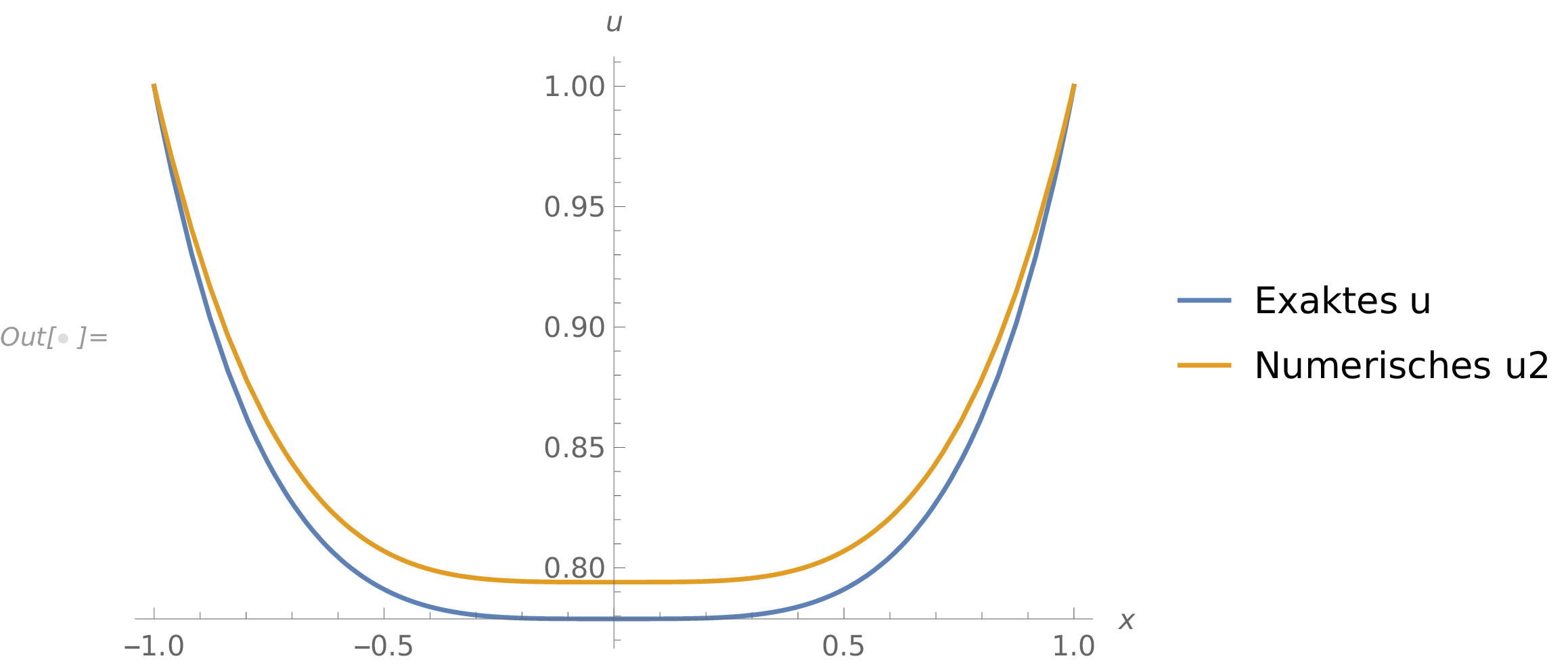
From the collocation condition we now get a linear system of equations with three unknowns: \begin {equation} \begin {split} R(x_0; a_0, a_1, a_2) \equiv & -\frac {659}{256} a_0 + \frac {1683}{512} a_1 - \frac {1171}{1024} a_2 - \frac {49}{64} = 0 \\ R(x_1; a_0, a_1, a_2) \equiv & -2(a_0-a_2) = 0 \\ R(x_2; a_0, a_1, a_2) \equiv & -\frac {659}{256} a_0 - \frac {1683}{512} a_1 - \frac {1171}{1024} a_2 - \frac {49}{64} = 0 \end {split} \label {eq:residual-num-example} \end {equation} The solution of these equations results in \begin {equation} a_0 = -\frac {784}{3807}, \quad a_1 = 0 \quad \text {and} \quad a_2 = a_0. \end {equation} Figure 5.1 shows the “numerical” solution \(u_2(x)\) in comparison with the exact solution \(u(x)\).
In the numerical example shown here, both the basis functions and the strategy for minimizing the residual can be varied. In the course of this lecture, we will establish the finite elements as basis functions and use the Galerkin method as minimization strategy. To do this, we must first discuss properties of possible basis functions.
Note: The example shown here is a simple case of discretization. We have gone from a continuous function to the discrete coefficients \(a_0\), \(a_1\), \(a_2\).
5.4 Numerical solution
It is straightforward to arrive at a numerical solution with Python. The first step is to realize that Eqs. \eqref{eq:residual-num-example} is a system of linear equations. We can generally write \begin {equation} \begin {split} K_{00} a_0 + K_{01} a_1 + K_{02} a_2 &= f_0 \\ K_{10} a_0 + K_{11} a_1 + K_{12} a_2 &= f_1 \\ K_{20} a_0 + K_{21} a_1 + K_{22} a_2 &= f_2 \label {eq:explicit-matrix-vector-product} \end {split} \end {equation} with the coefficients \(K_{ij}\) and \(f_i\) from Eqs. \eqref{eq:residual-num-example}. Equations \eqref{eq:explicit-matrix-vector-product} are the product of the matrix \(\t {K}\) with the vector \(\v {a}\) of unknown coefficients, i.e. \begin {equation} \t {K}\cdot \v {a} = \v {f}. \end {equation} The coefficients \(a_i\) are thefore given by the solution of this system of linear equations. The matrix \(\t {K}\) is called the system matrix and \(\v {f}\) is the load vector.
In Python, we first need to enter the matrix coefficient
1K00 = -659/256 2K01 = 1683/512 3K02 = -1171/1024 4f0 = 49/64 5 6K10 = -2 7K11 = 0 8K12 = 2 9f1 = 0 10 11K20 = -659/256 12K21 = -1683/512 13K22 = -1171/1024 14f2 = 49/64
System matrix and load vector can be defined as a numpy-arrays
1import numpy as np 2K = np.array([[K00, K01, K02], 3 [K10, K11, K12], 4 [K20, K21, K22]]) 5f = np.array([f0, f1, f2])
and we can directly compute the solution with the standard solver for systems of linear equations,
1a0, a1, a2 = np.linalg.solve(K, f)