Chapter 3
Transport theory
Context: This chapter introduces the foundations of transport theory, in particular how to balance conserved quantity. This leads to the continuity equation, which describes conservation of a quantity. We start from a classic and illustrative example, the diffusion of particles suspended in a liquid.
3.1 Diffusion and drift
Diffusive transport can be easily understood through the concept of a “random walk”, which describes the stochastic movement of particles. This phenomenon, known as random motion, was first observed by the botanist Robert Brown (1773–1858), who noticed the erratic movement of pollen grains suspended in water. His observations led to the term Brownian motion or Brownian molecular motion, though Brown himself was unaware of the existence of molecules at the time. Initially, he believed the movement resulted from active biological processes (the “force of life” in the pollen), but he later demonstrated that inanimate matter also exhibits this random motion. Today, we understand that this movement is caused by thermal fluctuations, where molecules randomly collide with suspended particles, propelling them in random directions. This explanation, which depends on the existence of atoms, was popularized in 1905 by Albert Einstein (Einstein, 1905).
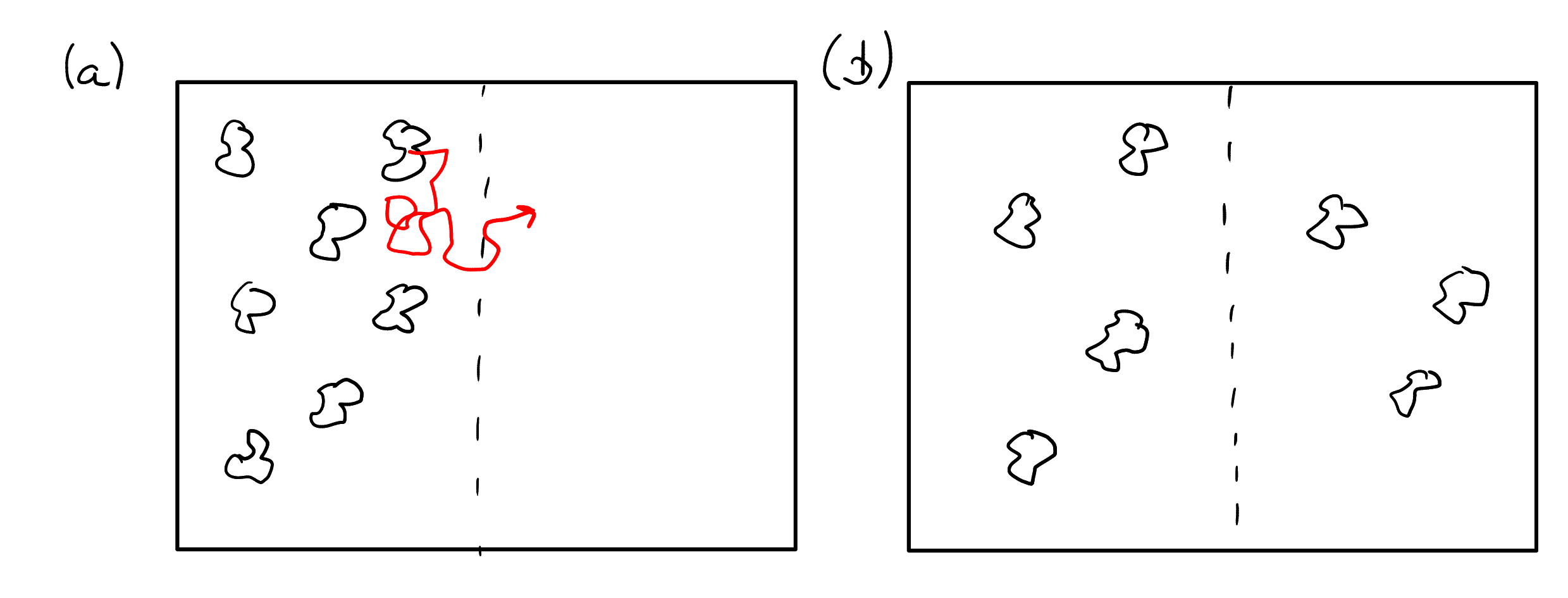
Brownian molecular motion leads to diffusive transport. Figure 3.1 shows a simple qualitative thought experiment. The configuration in Fig. 3.1a shows a localization of the “pollen” in the left half of the domain shown. Due to their random movement (shown as an example by the red line in Fig. 3.1a), some of the pollen will cross the dashed boundary line into the right half and also come back again. After a certain time, the initial state can no longer be identified and the pollen are distributed throughout the domain (Fig. 3.1b). The concentration is now constant. The pollen continue to move, but on average the same number of pollen move to the left as to the right. In the case shown in Fig. 3.1a, this left/right symmetry is broken which leads to a finite flux to the right.
This thought experiment can be easily formalized mathematically. We consider a particle that performs a random movement in one dimension. We start with a particle that randomly jumps back and forth on a straight line. The straight line lies along the x-direction. The particle can only move to predetermined positions on the x-axis, which we denote by \(x_j\) and which are equidistant, \(x_j-x_{j-1}=\Delta x\) for \(j\in \mathbb {Z}\) (see Fig. 3.2).
A particle jumps to the left with a probability \(p\) and to the right with a probability probability \(q\). In addition, we have the probability of finding a particle at time \(t\) at position \(x\), given on the 1D grid by the function \(P(x_j,t)\).
3.1.1 Diffusion
We first consider the case \(p=q=1/2\), i.e. that the probabilities for the jumps to the left and right are identical. We assume that the particles jump from site to its neighbors in a discrete, finite and constant time step \(\tau \). Then the probability of finding a particle at time \(t+\tau \) at location \(x\) is \begin {equation} P(x,t+\tau )=\frac {1}{2}P(x+\Delta x,t)+\frac {1}{2}P(x-\Delta x,t), \end {equation} where \(P(x-\Delta x,t)\) is the probability of finding a particle at position \(x-\Delta x\) and \(P(x+\Delta x,t)\) the probability of finding a particle at \(x+\Delta x\), both at time \(t\).
By subtracting \(P(x,t)\) on both sides and dividing by \(\tau \), we obtain the following equivalent form: \begin {equation} \frac {P(x,t+\tau )-P(x,t)}{\tau } = \frac {\Delta x^2}{2\tau }\frac {P(x+\Delta x,t)-2P(x,t)+P(x-\Delta x,t)}{\Delta x^2} \end {equation} We can now make the limit transition to the “continuum”. Taking \(\tau \rightarrow 0\) and at the same time \(\Delta x\rightarrow 0\) while maintaining \begin {equation} \lim _{\Delta x\rightarrow 0, \tau \rightarrow 0}\frac {\Delta x^2}{2\tau }=D \end {equation} yields \begin {equation} \frac {\partial P(x,t)}{\partial t}=D\frac {\partial ^2 P(x,t)}{\partial x^2}. \end {equation} This is the well-known diffusion equation.
Note: Given a function \(f(x,y)\), we write the partial derivative of this function with respect to \(x\) as \begin {equation} \frac {\partial f}{\partial x} = \partial _x f. \end {equation} The second derivative with respect to \(x\) is then \begin {equation} \frac {\partial ^2 f}{\partial x^2} = \partial ^2_x f. \end {equation} Mixed derivatives are written as \begin {equation} \frac {\partial ^2 f}{\partial x \partial y} = \partial _x\partial _y f. \end {equation} The total derivative is indicated with the letter \(\dif \), e.g. \begin {equation} \label {eq:totalderiv} \frac {\dif f}{\dif t} = \frac {\partial f}{\partial x} \frac {\partial x}{\partial t} + \frac {\partial f}{\partial y} \frac {\partial y}{\partial t} \end {equation} for \(f=f(x,y)\), \(x=x(t)\) and \(y=y(t)\).
Sometimes the prime is used to a indicate derivative, e.g. \(f'(x)=\dif f/\dif x\) is the derivative of \(f\). It is common to indicate the derivative with respect to time by a dot, i.e. given \(f(t)\) the derivative \(\dot {f}(t)=\dif f/\dif t\). We will use these notations occasionally for brevity but point out that writing the differential operator explicitly is less ambiguous. In particular, for functions of more than one variable the differential operator allows us to distinguish clearly between total and partial derivatives.
In multiple dimensions, the second derivative becomes the Laplace operator \(\nabla ^2\), \begin {equation} \frac {\partial P(x,t)}{\partial t}=D \nabla ^2 P(x,t). \label {eq:diffusion} \end {equation} This equation is only correct if the diffusion constant is actually constant and does not vary spatially.
Note: The operator \(\nabla \) is a vector of the partial derivatives in the Cartesian direction, i.e. \begin {equation} \nabla = \begin {pmatrix} \partial /\partial x \\ \partial /\partial y \\ \partial /\partial z \end {pmatrix}. \end {equation} Applying it to a scalar function \(f(x,y,z)\) yields the gradient, \begin {equation} \nabla f= \text {grad}\,f = \begin {pmatrix} \partial f/\partial x \\ \partial f/\partial y \\ \partial f/\partial z \end {pmatrix}. \end {equation} The Laplacian is sometimes denoted by \(\nabla ^2\) (often in the anglo-saxon literature) or \(\Delta \) (e.g. in the German literature). It is explicitly given by \begin {equation} \Delta = \nabla ^2 = \frac {\partial ^2}{\partial x^2} + \frac {\partial ^2}{\partial y^2} + \frac {\partial ^2}{\partial z^2}. \end {equation} We will use \(\nabla ^2\) for the Laplacian throughout this text.
3.1.2 Drift
What happens if the probabilities for the jumps to the right or left are not equal, \(p\ne q\) (but of course \(p+q=1\) because we would be creating or destroying particles if this condition was violated)? We still assume discrete, uniform time steps and equidistant sampling points.
In this case, we have \begin {equation} P(x,t+\tau )=pP(x+\Delta x,t)+qP(x-\Delta x,t) \end {equation} which yields \begin {equation} \frac {P(x,t+\tau )-P(x,t)}{\tau }=\frac {\Delta x^2}{\tau }\frac {pP(x+\Delta x,t)-P(x,t)+qP(x-\Delta x,t)}{\Delta x^2}. \label {eq:driftpq} \end {equation} This can be simplified by writing \begin {equation} p=\frac {1}{2}-\varepsilon \quad \text {and}\quad q=\frac {1}{2}+\varepsilon \quad \text {with}\quad 0\le |\varepsilon |\le \frac {1}{2} \quad \text {or}\quad 2\varepsilon = q-p, \end {equation} where \(\varepsilon \) now indicates how much more likely a jump to right is than to the left. A positive \(\varepsilon \) therefore means that the particles will move to the right on average – this is called drift. We can now write Eq. \eqref{eq:driftpq} using \(\varepsilon \), giving \begin {equation} \begin {split} \frac {P(x,t+\tau )-P(x,t)}{\tau }=& \frac {\Delta x^2}{2\tau }\frac {P(x+\Delta x,t)-2P(x,t)+P(x-\Delta x,t)}{\Delta x^2}\\\ &-\frac {2\varepsilon \Delta x}{\tau }\frac {P(x+\Delta x,t)-P(x-\Delta x,t)}{2\Delta x}. \end {split} \end {equation} In the limit \(\tau \rightarrow 0\) and \(\Delta x\rightarrow 0\) we require \begin {equation} \lim _{\Delta x\rightarrow 0, \tau \rightarrow 0}\frac {\Delta x^2}{2\tau }=D \quad \text { and }\quad \lim _{\Delta x\rightarrow 0, \tau \rightarrow 0}\frac {2\varepsilon \Delta x}{\tau }=v \label {eq:limit2} \end {equation} and thus obtain the drift-diffusion equation \begin {equation} \frac {\partial P(x,t)}{\partial t}=\left (D\frac {\partial ^2}{\partial x^2} -v\frac {\partial }{\partial x}\right ) P(x,t). \label {eq:driftdiffusion} \end {equation} Here, the first summand on the right-hand side again describes the diffusion process. The second summand is a drift process and \(v\) is a constant drift velocity. (From Eq. \eqref{eq:limit2} and \eqref{eq:driftdiffusion} it can be seen that the unit of \(v\) corresponds exactly to a velocity.) It is the speed at which the particle moves (on average) along the \(x\)-axis.
Note: The motion of our particle was modeled using a probability density \(P\). In the thermodynamic limit, i.e. for many particles (usually of the order of Avogadro’s number \(N_\text {A}\sim 10^{23}\)), this probability becomes the (mass) density \(\rho \) or the concentration (number density) \(c\). We can therefore simply replace the probability \(P\) in the above equations with a concentration \(c\). The reason for this is that we can write the concentration as an ensemble mean, \begin {equation} c(x, t) = \langle 1 \rangle (x, t), \end {equation} where the mean value is defined as \begin {equation} \langle f(x) \rangle (x, t) = f(x) P(x, t). \end {equation}
3.2 Continuity
The equations \eqref{eq:diffusion} and \eqref{eq:driftdiffusion} mix two concepts that we want to treat separately now: The conservation of the number of particles (continuity) and the process that leads to a flow of particles (diffusion or drift). The number of particles is conserved simply because we cannot create atoms out of nothing or destroy them into nothing. If we have a certain number of particles \(N_{\text {tot}}\) in our overall system, we know that this number \begin {equation} N_{\text {tot}}(t) = \int \dif ^3r \, c(\v {r}, t) \label {eq:ntot} \end {equation} cannot change over time: \(\dif N_{\text {tot}}/\dif t=0\). The integral in Eq. \eqref{eq:ntot} is carried out over the total volume of our system, essentially the physical world of the model.
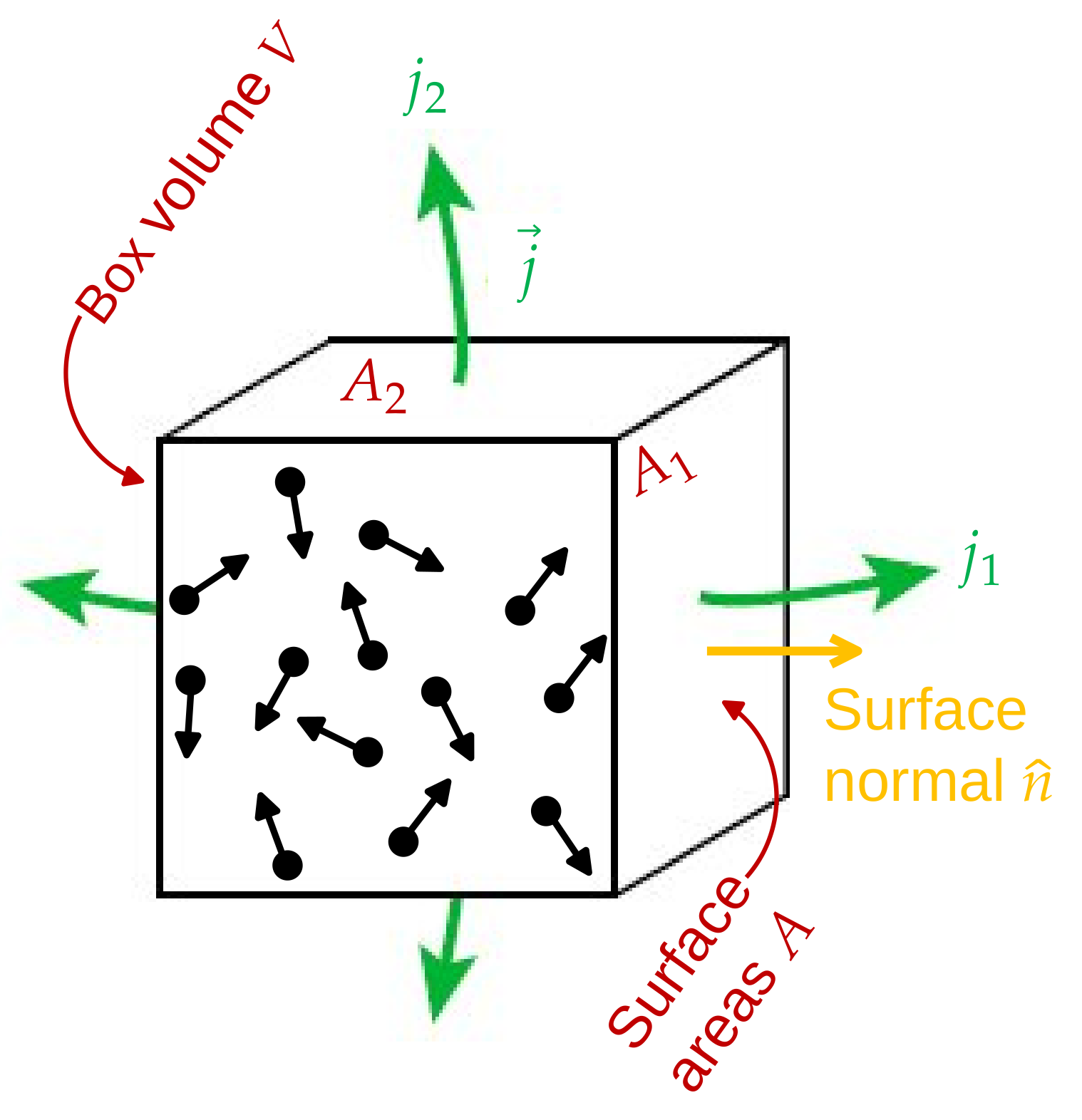
For a small section of our physical world with volume \(V\), the number of particles can change because they can flow through the walls of this sample volume (see Fig. 3.3). The change in the number of particles within \(V\) is given by \begin {equation} \dot {N}_V = \frac {\partial }{\partial t} \int _V \dif ^3r \, c(\v {r}, t) = \int _V \dif ^3r \, \frac {\partial c}{\partial t}. \label {eq:nchange} \end {equation} However, the change \(\dot {N}_V\) must also be given by the number of particles flowing through the side walls. For a cube (Fig. 3.3) with six walls, we can simply count the number of particles through each of the walls per unit time. It is approximately given \begin {equation} \begin {split} \dot {N}_V = & - j_{\text {right}} A_{\text {right}} - j_{\text {left}} A_{\text {left}} \\ & - j_{\text {above}} A_{\text {above}} - j_{\text {bottom}} A_{\text {bottom}} \\ & - j_{\text {front}} A_{\text {front}} - j_{\text {back}} A_{\text {back}} \end {split} \label {eq:dotN} \end {equation} if the walls are small enough so that \(j\) is almost constant over \(A\). We have, in passing, introduced the current density \(j\) with unit number of particles/time/area. The quantities \(j A\) are hence the number of particles flowing per unit time through one of the walls with are \(A\).
The scalar current density \(j\) describes the current flowing out of the surface. For a general vectorial current density \(\v {j}\), which indicates the strength and direction of the particle current, the total current density flowing out of the volume through wall \(i\) is given by \(j_i = \v {j}_i \cdot \hat {n}_i\), where \(\hat {n}_i\) is the normal vector pointing outwards on wall \(i\). The current through the wall is therefore only the component of \(\v {j}\) that is parallel to the surface normal (or perpendicular to the wall). With this argument, we can generalize the expression for the change in number of particles to \begin {equation} \dot {N}_V = -\int _{\partial V} \dif ^2r \, \v {j}(\v {r})\cdot \hat {n}(\v {r}) \label {eq:flux} \end {equation} where \(\partial V\) denotes the surface area of the volume \(V\). This equation explicitly indicates that both the flux \(\v {j}\) and the surface normal \(\hat {n}\) depend on the position \(\v {r}\) on the surface.
Alternatively, we can also group the change in the number of particles, Eq. \eqref{eq:dotN}, as follows: \begin {equation} \begin {split} \dot {N}_V = & - (j_{\text {right}} + j_{\text {left}}) A_{\text {right/left}} \\ & - (j_{\text {top}} + j_{\text {bottom}}) A_{\text {top/bottom}} \\ & - (j_{\text {front}} + j_{\text {rear}}) A_{\text {front/back}} \end {split} \end {equation} Here we have used the fact that \(A_{\text {right}}=A_{\text {left}}\equiv A_{\text {right/left}}\). But now \begin {equation} \begin {split} j_{\text {right}} &= \hat {x} \cdot \v {j}(x+\Delta x/2,y,z) = j_x(x+\Delta x/2,y,z) \quad \text {and} \\ j_{\text {left}} &= -\hat {x} \cdot \v {j}(x-\delta x/2,y,z) = -j_x(x-\delta x/2,y,z) \end {split} \end {equation} since \(\hat {n}=\hat {x}\) for the right wall but \(\hat {n}=-\hat {x}\) for the left wall. Here, \(\hat {x}\) is the normal vector along the \(x\)-axis of the coordinate system. The sign of the surface normal is therefore reversed between the right and left surfaces. The same applies to the top/bottom and front/back walls. We can further rewrite this equation as \begin {equation} \begin {split} \dot {N}_V = & - \frac {j_x(x+\Delta x/2,y,z) - j_x(x-\Delta x/2,y,z)}{\Delta x} V \\ & - \frac {j_y(x,y+\Delta y/2,z) - j_y(x,y-\Delta y/2,z)}{\Delta y} V \\ & - \frac {j_z(x,y,z+\Delta z/2) - j_z(x,y,z-\Delta z/2)}{\Delta z} V, \end {split} \label {eq:dotNdiscr} \end {equation} since \(V=A_{\text {right/left}}\Delta x=A_{\text {top/bottom}}\Delta y=A_{\text {front/back}}\Delta z\). However, the factors in front of the volume \(V\) in Eq. \eqref{eq:dotNdiscr} are now exactly the difference quotients of the flows \(j_i\), in the \(x\), \(y\) and \(z\) directions respectively. For small volumes (and small \(\Delta x\), etc.) this becomes \begin {equation} \dot {N}_V = -\int _{V} \dif ^3r \, \nabla \cdot \v {j}(\v {r}). \label {eq:flux2} \end {equation} We have just heuristically derived the divergence theorem (see also Eq. \eqref{eq:divergencetheorem}) to express Eq. \eqref{eq:flux} as a volume integral.
Note: We have expressed the divergence of a vectorial field \(\v {f}(\v {r})\) through the nabla operator, \begin {equation} \nabla \cdot \v {f} = \text {div}\, \v {f} = \frac {\partial f_x}{\partial x} + \frac {\partial f_y}{\partial y} + \frac {\partial f_z}{\partial z} \end {equation} The divergence theorem is an important result of vector calculus. It converts an integral over a volume \(V\) into an integral over the surface \(\partial V\) of this volume. For a vector field \(\v {f}(\v {r})\) applies: \begin {equation} \int _V \dif ^3 r\, \nabla \cdot \v {f}(\v {r}) = \int _{\partial V} \dif ^2 r\, \v {f}(\v {r}) \cdot \hat {n}(\v {r}) \label {eq:divergencetheorem} \end {equation} Here \(\hat {n}(\v {r})\) is the normal vector which points outwards on the edge \(\partial V\) of the volume \(V\). Note that in one dimension this reduces to \begin {equation} \int _a^b \dif x\, \frac {\partial f}{\partial x} = f(b) - f(a), \end {equation} which is the integration rule we all know from high school. The divergence theorem is hence a generalization of this integration rule to functions of many variables.
Equation \eqref{eq:nchange} and \eqref{eq:flux2} together result in \begin {equation} \int _V \dif ^3r \, \left \{\frac {\partial c}{\partial t}+\nabla \cdot \v {j}\right \} = 0. \label {eq:continuityweak} \end {equation} Since this applies to any volume \(V\), the equation \begin {equation} \frac {\partial c}{\partial t}+\nabla \cdot \v {j} = 0 \label {eq:continuity} \end {equation} must also hold. This equation is called continuity equation. It describes the conservation of the number of particles or the mass of the system.
Note: In the derivation presented here, we have already implicitly used the strong formulation and a weak formulation of a differential equation. Equation \eqref{eq:continuity} is the strong formulation of the continuity equation. This requires that the differential equation is satisfied for every spatial point \(\v {r}\). A corresponding weak formulation is Eq. \eqref{eq:continuityweak}. Here it is only required that the equation is fulfilled in a kind of mean value, here as an integral over a sample volume \(V\). Within the volume, the strong form need not be satisfied, but the integral over deviations from the strong form (which we will later call “residuum”) must vanish. The weak formulation is thus an approximation for finite sample volumes \(V\). In many numerical approaches, a weak equation is solved exactly for a certain (approximate) initial function.
We can still require that “particles” are produced within our sample volume. In the current interpretation of the equation, this could be, for example, chemical reactions that convert one type of particle into another. An identical equation applies to heat transport, because just like particle numbers, also the energy is a conserved quantity. Here, a source term would be the production of heat, e.g. by a heating element. Given a flow \(Q\) (with unit number of particles/time/volume), the particle or heat source, the continuity equation can be extended to \begin {equation} \frac {\partial c}{\partial t}+\nabla \cdot \v {j} = Q. \label {eq:continuitywithsource} \end {equation} The continuity equation with source term is also sometimes referred to as the balance equation.
Note: Equation \eqref{eq:continuitywithsource} describes the change in concentration \(c\) over time. A related question is what the concentration \(c\) becomes after a very long time - when a dynamic equilibrium has been reached and the concentration no longer varies but is stationary. This equilibrium is then characterized by the fact that \(\partial c/\partial t=0\). The equation \begin {equation} \nabla \cdot \v {j} = Q \end {equation} is the stationary variant of the continuity equation.
3.2.1 Drift
Let us come back to transport processes, first to drift. If all particles in our sample volume move with the velocity \(\v {v}\), this leads to a particle flow \begin {equation} \v {j}_{\text {Drift}} = c \v {v}. \label {eq:drift} \end {equation} When inserted into the continuity equation \eqref{eq:continuity}, this results in the drift contribution to the drift-diffusion equation \eqref{eq:driftdiffusion}.
3.2.2 Diffusion
From our thought experiment above, it is clear that the diffusion current must always point in the direction of lower concentration, i.e. in the direction opposite to the gradient \(\nabla c\) of the concentration. The corresponding current is given by \begin {equation} \v {j}_{\text {Diffusion}} = - D \nabla c. \label {eq:stationary} \end {equation} When inserted into the continuity equation \eqref{eq:continuity}, this results in the diffusion equation \eqref{eq:diffusion}.
The entire drift-diffusion equation therefore has the form \begin {equation} \frac {\partial c}{\partial t} + \nabla \cdot \left (-D\nabla c + c\v {v}\right )=0. \label {eq:drift-diffusion-full} \end {equation} In contrast to equations \eqref{eq:diffusion} and \eqref{eq:driftdiffusion}, this equation also applies if the diffusion constant \(D\) or drift velocity \(\v {v}\) varies spatially.
Note: We have introduced transport theory here in terms of a particle concentration \(c\). However, similar continuity equations describes the conservation of other quantities, in particular momentum and energy. Continuity of momentum leads to the Navier-Stokes equations. The continuity equation for the energy leads to the heat conduction equation.