Chapter 1
Introduction
Context: The term simulation refers to the numerical (computer-aided) solution of models. In this introductory chapter, we discuss how models of physical reality are built and present different classes of models. These models are usually described mathematically by means of differential equations, i.e. “simulation” is often (but not always) the numerical solution of a set of ordinary or partial differential equations.
1.1 Models
Models are approximations for the behavior of the physical world at certain length scales. For example, a model that explicitly describes atoms “lives” on length scales on the order of \(\text {nm}\) and may be appropriate to describe the growth of thin films in semiconductor manufacturing. We would not want to describe a macroscopic system or phenomenon that lives on scales of \(\sim \text {mm}\) or beyond, such as how water flows out of a tap or how an airplane wing bends during takeoff, with such a model. Key to carrying out simulations is therefore the ability to match the physical phenomenon we want to describe with the appropriate model and the mathematical method required for its solution.
Note: While we could describe even macroscopic systems with atomic-scale models, this is typically prohibited by the computer resources available to us. Macroscopic systems consist of more than \(10^{23}\) (Avogadro’s number) atoms, whose positions we would not be able to fit into present day computers. In addition, the gist of the question we want to answer may be hidden in such a fine-grained atomic-scale model like the legendary needle in a haystack.
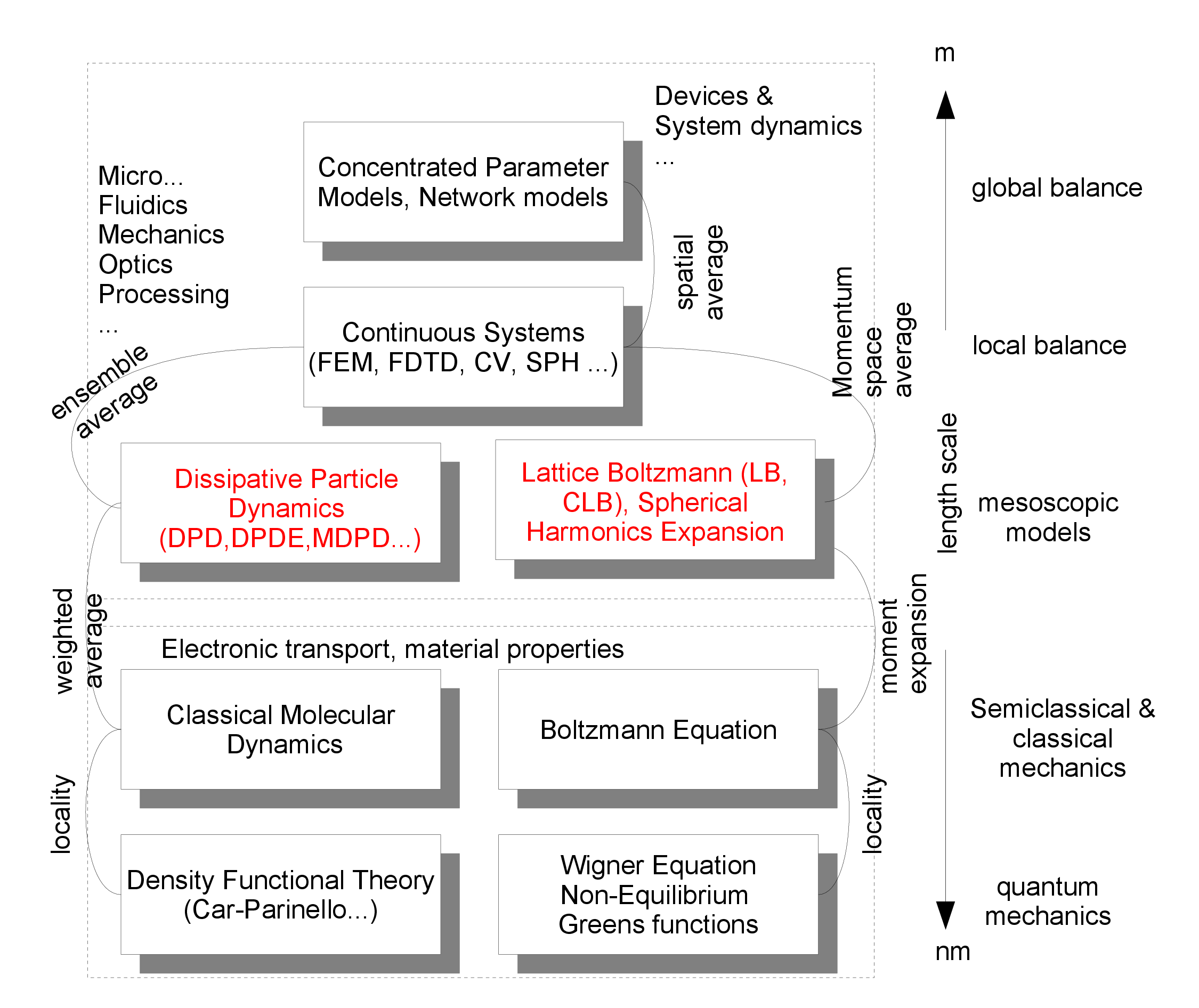
Figure 1.1 shows on the vertical axis length scales and classes of models that live on these scales. On the shortest length scale, a quantum mechanical description is usually necessary. This means that if we want to resolve the world with Å resolution, we find ourselves at the level of quantum mechanics and all underlying models are of a quantum mechanical nature. Underlying quantum mechanics is the Schrödinger equation, whose (approximate) solution is implemented in various methods, such as density functional theory (Martin, 2004), a many-body description of the quantum mechanical electronic system. If we get rid of modeling the electron explicitly, we arrive at a class of simulation methods often referred to as molecular dynamics (Allen and Tildesley, 1989). The key mathematical object in molecular dynamics is the set of positions and velocities of all atoms, which means we have to introduce three position and three velocity variables for each of the \(n\) interacting particles. In contrast, in a quantum mechanical many-body description we are dealing with a field with three \(n\) position variables each, namely \(\Psi (\v {r}_1,\v {r}_2,\dots ,\v {r}_n;t)\). This illustrates that formulating models on larger length scales requires some form of coarse-graining, i.e. removing information from a smaller scale model.
Note:
- \(1\,\r {A}=10^{-10}\,\text {m}\)
- The atoms that constitute our physical world are held together by quantum mechanics. Models based on quantum mechanical principles are also called ab-initio (“from the beginning”) or first principles models. The fundamental equation that describes quantum mechanical objects is the Schrödinger equation. It is itself is in fact already an approximation, despite the fact that models derived from it are called first principles models!
- The single-particle Schrödinger equation is \(i\hbar \frac {\partial }{\partial t} \Psi (\v {r},t) = \hat {H} \Psi (\v {r},t)\). This is a partial differential equation for the location- and time-dependent scalar matter field \(\Psi (\v {r},t)\), with Planck’s constant \(\hbar \) and the Hamilton operator \(\hat {H}\), which contains the details of the model. The solution of an equation of motion for many interacting particles, as described by a wavefunction with mathematical structure \(\Psi (\v {r}_1,\v {r}_2,\dots ,\v {r}_n;t)\), is incomparably more complicated.
- “Semiclassical“ means that the motion of the particles is calculated according to classical mechanics, but the interactions between the particles are derived from quantum mechanical laws. This is of course an approximation that needs to be justified.
- “Mesoscopic” means that the model has an internal length scale and/or thermal fluctuations are important. These models usually operate on length scales above the atomic scale (\(\sim \) nm) but below the scales of our perception of the environment (\(\sim \) mm).
- “Balance” means that the core of the description is a conserved quantity. Conserved are e.g. particle numbers or mass (that is typically automatically conserved in models that have particles as the core mathematical object). The balance equation or balancing then simply counts the particles that flow into or out of a volume element over a certain time interval. Other conserved variables that can be balanced are momentum and energy. The balance equation is also called the continuity equation.
At the level of semiclassical and classical mechanics, also referred to as the kinetic level, models are either described by molecular dynamics or by the equation of motion of the single-particle probability density in phase space \(f(\v {r},\v {p})\) - with location \(\v {r}\) and momentum \(\v {p}\) as independent variables. In the second case, we have a function \(f(\v {r}(t),\v {p}(t),t)\) which depends on time both explicitly and implicitly via \(\v {r}(t)\) and \(\v {p}(t)\). Let us assume that we need to discretize \(f(\v {r}(t),\v {p}(t),t)\) on regular grid of discrete sampling points. At a low resolution of \(10\) points per variable, this corresponds to already \(10,000,000\) interpolation points. This may be manageable, but the resolution of such a model would not particularly good. This undertaking is therefore rather useless. We do not want to conceal the fact that there are methods for the numerical solution to the two problems described above, but these will not be discussed in detail in this class.
1.2 Particles
We can therefore roughly distinguish between two types of models: Models that have individual discrete elements, for example particles (atoms, molecules, grains, etc.), as their central mathematical objects and models that have continuous fields (electrostatic potential, ion concentrations, mechanical stresses and strains) as the central objects. In the first type of model, evolution equations are formulated for discrete properties defined on the particles, such as their positions \(\v {r}_i\) and velocities \(\v {v}_i\).
For example, to describe the kinetics of these particles, we could solve Newton’s equations of motion. This means that for each of the \(n\) particles we have to formulate \(6\) ordinary differential equations (ODEs), which are coupled to each other, namely: \begin {equation} \dot {\v {r}}_i(t)=\v {v}_i(t)=\frac {\v {p}_i(t)}{m_i} \label {eq:posupdate} \end {equation} This is the equation for the trajectory of the particle \(i\) in space. Since \(\v {r}_i\) is a vector, Eq. \eqref{eq:posupdate} is a system of \(3\) ordinary differential equations. differential equations. The velocity \(\v {v}_i\) of the particle \(i\) at time \(t\) is also subject to a system of differential equations, expressed most simply using the momentum \(\v {p}_i\), \begin {equation} \dot {\v {p}}_i(t)=\v {F}_{i}(t), \label {eq:velupdate} \end {equation} where \(\v {F}_{i}(t)\) is the force acting of particle \(i\) at time \(t\). Equation \eqref{eq:velupdate} describes the temporal evolution of the momentum of the particle \(i\). Equation \eqref{eq:posupdate} and \eqref{eq:velupdate} are each \(3\times n\) coupled ordinary differential equations. If, for example, we want to describe the movement of all molecules in a liter of water by a simulation, this is impossible due to the large number of equations and we must switch to a description using balance equations and fields.
Newton’s equations of motion \eqref{eq:posupdate} and \eqref{eq:velupdate} are by their nature basic physical principles. They apply to atoms or planets. The nature of the force itself, \(\v {F}_{i}\) in the equations above, depends on the nature of the physical system that we study. It is not necessarily a fundamental interaction, such as gravity, but may emerge from a complex interplay of multiple physical mechanisms. A simple example is the Lennard-Jones interaction with interaction energy \begin {equation} V_{ij} = 4\varepsilon \left [ \left (\frac {\sigma }{r_{ij}}\right )^{12} - \left (\frac {\sigma }{r_{ij}}\right )^{6}\right ] \label {eq:lj_potential} \end {equation} and force \begin {equation} \v {F}_{ij} = -4\varepsilon \left [ 12\left (\frac {\sigma ^{12}}{r_{ij}^{13}}\right ) - 6\left (\frac {\sigma ^{6}}{r_{ij}^{7}}\right )\right ]\hat {r}_{ij}. \label {eq:lj} \end {equation} We have written this in terms of a pair interaction and assumes that forces are pair-wise additive, meaning the total force on particle \(i\) is given by \(\v {F}_i=\sum _j \v {F}_{ij}\). The quantity \(r_{ij}\) is the distance between the particles (here atoms or molecules) \(i\) and \(j\), and \(\hat {r}_{ij}\) is the normal vector pointing from one to the other. The term \(\propto r^{-13}\) describes the repulsion of the atoms due to the Pauli exclusion principle and the term \(\propto r^{-7}\) describes the attraction of the atoms due to the London dispersion interaction (Müser et al., 2023). Both interactions are based on fundamental physical principles, but the formulation Eq. \eqref{eq:lj} reduces these complex phenomena to a simple constituating law. Such laws are often called constitutive laws. The numerical solution of Newton’s equations of motion for atoms or molecules is called molecular dynamics simulation.
Note: The term constitutive law often appears in the context of field theories. For the Lennard-Jones potential, this term is rather unusual, but this law is nevertheless of a constitutive nature.
Another example of models with discrete elements are network models for electrical circuits. Here, an element links an electrostatic potential difference (energy difference) with a current, for example \begin {equation} i = u / R \label {eq:resistor} \end {equation} describes the current \(i\) that flows through a resistor \(R\) across which the voltage drops by \(u\). Such models are often referred to as “lumped-element models”. Equation \eqref{eq:resistor} naturally also has the quality of a constitutive law, as complex electronic processes are behind the individual parameter \(R\). For a fully formulated model of an electric circuits we also need Kirchhoff’s rules, that have the quality of balance equations. In Fig. 1.1, these models are therefore referred to as global balance models. “Lumped-element models” also lead to systems of ordinary differential equations, which are often solved numerically by explicit time propagation. Well-known representatives of this type of simulation software are, for example SPICE or MATLAB Simulink.
Such a global balance description is characterized by a lack of interest in local resolution. We are not interested in densities, but only in total masses, not in current densities but only in currents. This is best illustrated by the above-mentioned resistor whose contacts are at different potentials, which results in a current flow. We do not ask ourselves how the current is distributed in the resistor. We do not even ask whether the resistor is homogeneous or inhomogeneous. The model only requires the overall resistance \(R\), essentially modeling the resistor as a black box to which we assign the value of a single parameter. This approach is discussed in detail in electrical engineering and systems theory.
1.3 Fields
However, if we now realize that our black box is only insufficiently described with one parameter, then we need to replace it with a more complex models, for example an equivalent circuit with details that resolve the internal state of the component. This in turn can be taken so far, that a continuum is created at the end - we have arrived at a local balance descriptions. Staying with the example of flow, we need parameters such as conductivity (or for fluids viscosity or diffusivity), which now describe the resistance to flow locally. These parameters can be obtained from experiments or ab-initio simulations but are required as input to (or the “parameterization” of) the local balance description.
Local balance means that we can assign density, concentration, temperature or similar quantity to each point in space. However, this means that the temporal changes in the local degrees of freedom - i.e. the momentum or velocity - are constrained by a local, thermodynamic-equilibrium condition. (In thermodynamic equilibrium, the momentum satisfies a Maxwell-Boltzmann distribution.) This local equilibrium does not mean that we no longer have dynamics: If we think of a swarm of gas or liquid molecules, then their individual velocities follow an equilibrium distribution function, but their mean follows the balance equation. The dynamics are therefore averaged over a huge number of these particles. Local balance also does not mean that different temperatures or densities cannot exist at different locations. The differences in these parameters are then the driving forces of the dynamics – temperature gradients, density gradients, etc.
Such models fall into the category of field theories, and their mathematical description is based on partial differential equations. (This is in contrast to the ordinary differential equations of discrete models.) A transport theory is a specific class of field theory that is based on the balancing mass, momentum or energy and requiring constitutive laws for the description of the material behavior. These constitutive laws contain transport parameters such as the viscosity or diffusion constant. There are also field theories that have the character of a basic physical principle. This is, for example, the Schrödinger equation mentioned above or the Maxwell equations of electrodynamics.
1.4 Which model is the right one?
Choosing and formulating the right model is a form of art. Just because a theory is called “quantum mechanics” (and leaves one or the other in awe at its complexity), it does not necessarily offer the solution to the problem that we are trying to solve. Too much detail can even be a hindrance and we must constantly ask ourselves how much detail is necessary in model and simulation. We always need ask ourselves before we start a simulation: “Is a simulation of this complexity really necessary, or can I simplify the problem?” The simulation should be seen as a tool and not as an end in itself, according to the American mathematician Richard Wesley Hamming (*1915, \(\dagger \)1998): “The purpose of computing is insight, not numbers”.
Bibliography
M. P. Allen and D. J. Tildesley. Computer Simulation of Liquids. Oxford University Press, 1989.
R. M. Martin. Electronic Structure. Cambridge University Press, 2004.
M. H. Müser, S. V. Sukhomlinov, and L. Pastewka. Interatomic potentials: achievements and challenges. Advances in Physics: X, 8(1): 2093129, Jan. 2023.