Chapter 11
Finite elements in two and three dimensions
Context: We now generalize the results of the previous chapter to several dimensions. This has several technical hurdles: for the partial integration, we now have to use results from vector analysis, in particular the Gaussian theorem or Green identities. The discretization is carried out in the form of elements, usually triangles or tetrahedra. Due to this more complex geometry of the elements, a clean book-keeping of the indices, i.e. the distinction between global nodes, element nodes and elements, becomes important.
11.1 Differentiability
To illustrate how the requirement for differentiability can be reduced in higher-dimensional problems, and how we can thus use linear basis functions again, the Poisson equation is considered further here. In \(D\)-dimensions (usually \(D=2\) or \(D=3\)) the Poisson equation leads to the residual \begin {equation} R(\v {r}) = \nabla ^2 \Phi + \frac {\rho (\v {r})}{\varepsilon } = \nabla \cdot \left (\nabla \Phi \right ) + \frac {\rho (\v {r})}{\varepsilon } \label {eq:poissonreshighd} \end {equation} where \(\v {r}=(x,y,z,...)\) is now a \(D\)-dimensional vector denoting the position, and \(\nabla ^2\) is the Laplacian in \(D\) dimensions. The potential \(\Phi (\v {r})\) obviously also depends on the spatial position \(\v {r}\). The right-hand side of Eq. \eqref{eq:poissonreshighd} is explicitly written so that the combination of divergence and gradient that yields the Laplace operator can be recognized.
We now write down the weighted residual. The scalar product with a test function \(v(\v {r})\) yields \begin {align} (v(\v {r}), R(\v {r})) =& \int _\Omega \dif ^Dr\, v(\v {r}) \left ( \nabla ^2 \Phi + \frac {\rho (\v {r})}{\varepsilon } \right ) \\ =& \int _{\partial \Omega } \dif ^{D-1} r\, v(\v {r}) \left (\nabla \Phi \cdot \hat {n}(\v {r})\right ) -\int _\Omega \dif ^Dr\, \nabla v \cdot \nabla \Phi + \int _\Omega \dif ^Dr\, \frac {v(\v {r})\rho (\v {r})}{\varepsilon }, \label {eq:weakformhighd} \end {align}
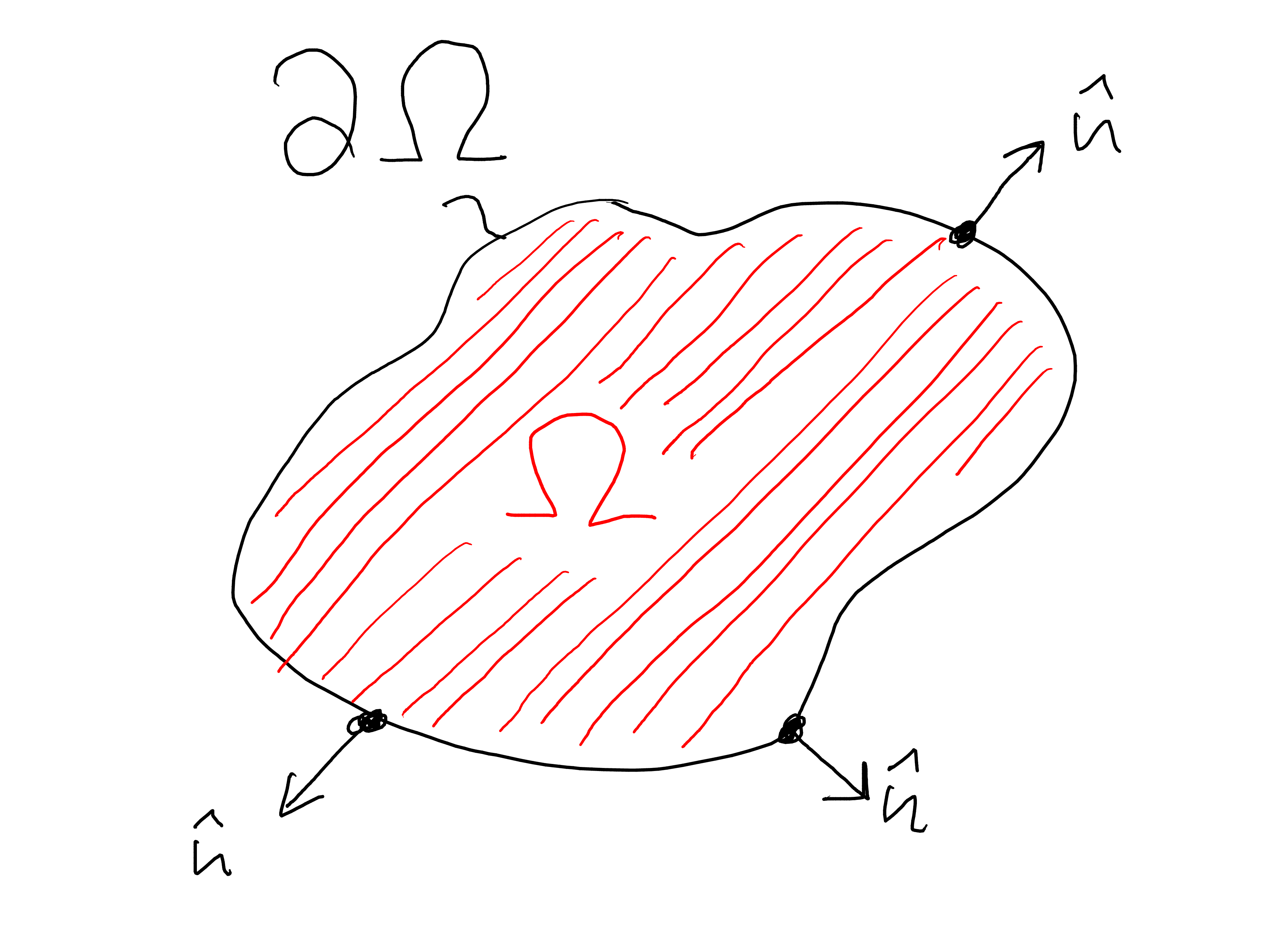
whereby the Green’s first identity has now been used to rewrite the surface or volume integral over \(\Omega \) and to transfer the gradient to the test function. Green’s identity takes on the role that partial integration had in the one-dimensional case. \(\hat {n}(\v {r})\) is the normal vector pointing outwards on the boundary \(\partial \Omega \) of the domain (see Fig. 11.1. The first term on the right-hand side of Eq. \eqref{eq:weakformhighd} will become important again when we want to specify Neumann boundary conditions on the boundary \(\partial \Omega \) of the domain. In the Dirichlet case, this term disappears.
Note: The Green identities are another important result of vector analysis. They follow from the Gaussian theorem. The Gauss theorem is \begin {equation} \int _\Omega \dif ^D r\, \nabla \cdot \v {f}(\v {r}) = \int _{\partial \Omega } \dif ^{D-1} r\, \v {f}(\v {r}) \cdot \hat {n}(\v {r}) \end {equation} where \(\partial \Omega \) denotes the \(D-1\) dimensional boundary of the \(D\)-dimensional integration domain \(\Omega \). Furthermore, \(\hat {n}(\v {r})\) is the normal vector perpendicular to the boundary pointing out of the integration domain (see also Fig. 11.1). We now apply Gauss’s theorem to a vector field \(\v {f}(\v {r})=\phi (\v {r})\v {v}(\v {r})\), where \(\phi (\v {r})\) is a scalar field and \(\v {v}(\v {r})\) is again a vector field. We obtain \begin {equation} \int _\Omega \dif ^D r\, \nabla \cdot \left (\phi \v {v}\right ) = \int _{\partial \Omega } \dif ^{D-1} r\, \left (\phi \v {v}\right ) \cdot \hat {n}. \end {equation} Due to the chain rule of differentiation, the following applies \begin {equation} \nabla \cdot \left (\phi \v {v}\right ) = \left (\nabla \phi \right )\cdot \v {v} + \phi \left (\nabla \cdot \v {v}\right ). \label {eq:chainrulevec} \end {equation} (The equation \eqref{eq:chainrulevec} is most easily seen if it is written in component form.) This leads to \begin {equation} \int _\Omega \dif ^D r\, \left (\nabla \phi \cdot \v {v} + \phi \nabla \cdot \v {v}\right ) = \int _{\partial \Omega } \dif ^{D-1} r\, \left (\phi \v {v}\right ) \cdot \hat {n}. \end {equation} With \(\v {v}(\v {r})=\nabla \psi \) we obtain the usual representation of Green’s first identity, \begin {equation} \int _\Omega \dif ^D r\, \left (\nabla \phi \cdot \nabla \psi + \phi (\v {r}) \nabla ^2\psi \right ) = \int _{\partial \Omega } \dif ^{D-1} r\, \left (\phi \nabla \psi \right ) \cdot \hat {n}. \end {equation}
In Eq. \eqref{eq:weakformhighd} the requirement for differentiability is now reduced. The Laplace operator, i.e. the second derivative, no longer appears in this equation. We just need to be able to calculate gradients of the test function \(v(\v {r})\) and the potential \(\Phi (\v {r})\).
11.2 Grid
We now need to choose suitable basis functions so that the Galerkin conditions yield a linear system of equations. It is useful to formulate the problem in terms of shape functions rather than basis functions. The rest of the theory in this chapter is developed for two-dimensional problems (\(D=2\)).
11.2.1 Triangulation
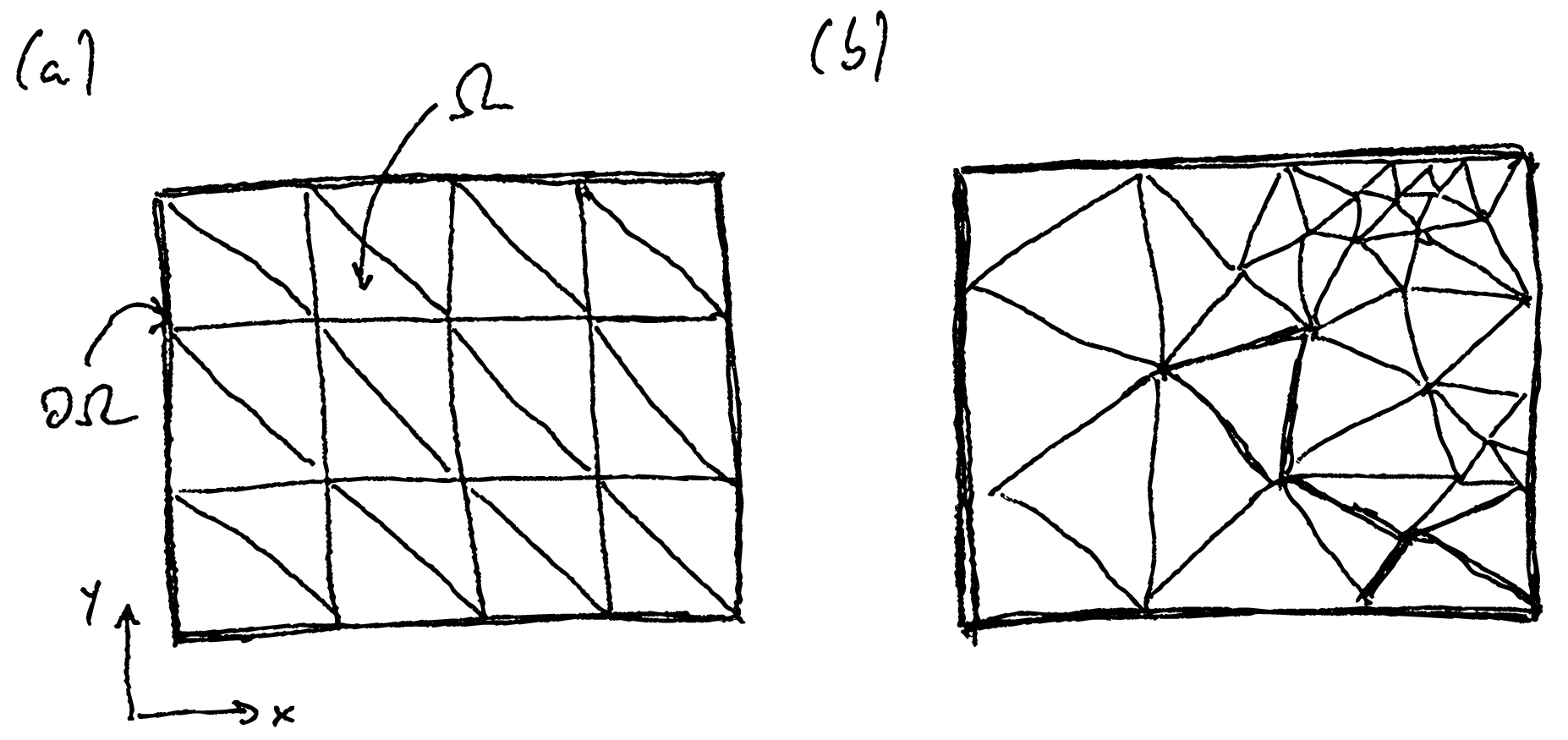
Before we can talk about these details of the basis functions, we need to discuss the decomposition of the simulation domain into elements. In two dimensions, these elements are usually (but not necessarily) triangles, i.e. one performs a triangulation of the domain. Figure 11.2 shows such a triangulation for a rectangular (2-dimensional) domain. This decomposition is also called the grid (or mesh), the individual triangles elements (or mesh elements), and the corners of the triangles nodes (or mesh nodes). The process of dividing the area is called meshing. We will work exclusively with structured grids, as shown in Fig. 11.2a. Many simulation packages also support unstructured grids as shown in Fig. 11.2b.
For this type of decomposition, too, the objective function \(\Phi (\v {r})\) can be approximated by a sum. We write \begin {equation} \Phi (x,y) \approx \Phi _N(x,y) = \sum _n a_n \varphi _n(x, y), \end {equation} where \(n\) is a unique node index. That is, the degrees of freedom or expansion coefficients \(a_n\) live on the nodes (with the positions \(\v {r}_n\)) of the simulation domain, and for a finite element basis, \(\Phi (\v {r}_n)=a_n\) will again apply, i.e., \(a_n\) is the function value on the corresponding node. The shape function then defines how this function value is interpolated between the nodes (i.e. across the triangles).
Note: In three dimensions, the decomposition of space usually takes place in tetrahedra. The meshing of such a three-dimensional area is highly non-trivial. All commercial finite element packages have meshing tools built in to take over or at least support this process. A free software solution for meshing complex geometries is Gmsh (https://gmsh.info/).
11.2.2 Structuring
Using a structured grid simplifies the assignment of a node index \(n\) or an element index \((n)\) to corresponding spatial positions. Figure 11.3 shows such a structured decomposition into \(M_x\times M_y\) (with \(M_x=L_x/\Delta x=3\) and \(M_y=L_y/\Delta y=3\)) boxes with two elements each. The grid contains \(N_x \times N_y\) (with \(N_x=M_x+1=4\) and \(N_y=M_y+1=4\)) nodes.
In this structured grid, we can infer the global index \(n_{\text {K}}\) of the nodes from their coordinates. Since the degrees of freedom live on the nodes, the global node index \(n_{\text {K}}\) later identifies a column or row from the system matrix. Let \(i,j\) be the (integer) coordinate of the node, then \begin {equation} n_{\text {K}} = i + N_x j \label {eq:linindex} \end {equation} the corresponding global node index. The node coordinates start at zero, i.e. \(i\in \{0,1,...,N_x-1\}\) and \(j\in \{0,1,...,N_y-1\}\). In the same way, we can deduce the element index \(n_{\text {E}}\) from the element coordinates \(k,l,m\), \begin {equation} n_{\text {E}} = k + 2(l + M_x m), \label {eq:linindexel} \end {equation} where \(l,m\) with \(l\in \{0,1,...,M_x-1\}\) and \(m\in \{0,1,...,M_y-1\}\) is the coordinate of the box and \(k\in \{0, 1\}\) indicates the element within a box. The factor \(2\) appears in Eq. \eqref{eq:linindexel} because there are two elements per box.
Note: The equations \eqref{eq:linindex} and \eqref{eq:linindexel} are probably the simplest mappings of coordinates to a linear, consecutive index. Other possibilities, which are also used in numerics, arise from the space-filling curves, such as the Hilbert or Peano curve. Space-filling curves sometimes have advantageous properties, such as the fact that coordinates that are close together also get indices that are close together. This leads to a more compact structure of the sparse system matrix and can bring advantages in the runtime of the algorithms. The reason for such runtime advantages is closely linked to the hardware, e.g. how the hardware organizes memory access and uses caches. Optimizing algorithms for specific hardware architectures is highly non-trivial and requires detailed knowledge of the computer architecture.
11.3 Shape functions
Our shape functions live on the individual triangles of the triangulation and must either be \(1\) at the respective node or disappear. We express the shape functions here using the scaled coordinates \(\xi = (x - x_0)/\Delta x\) and \(\eta = (y - y_0)/\Delta y\), where \(x_0\) and \(y_0\) is the origin of the respective box. Thus, in the lower left corner of the box, \(\xi =0\) and \(\eta =0\), and in the upper right corner, \(\xi =1\) and \(\eta =1\).
The shape functions for the element with local element index \((0)\) (see Fig. 11.3b) are \begin {align} N^{(0)}_0(\xi , \eta ) &= 1-\xi -\eta \\ \label {eq:formfunc1} N^{(0)}_1(\xi , \eta ) &= \xi \\ N^{(0)}_2(\xi , \eta ) &= \eta , \end {align}
where the subscript \(i\) in \(N_i\) denotes the local node index at which the shape function becomes \(1\). These shape functions are shown in Fig. 11.4. \begin {align} N^{(1)}_0(\xi , \eta ) &= \xi +\eta -1 \\ N^{(1)}_1(\xi , \eta ) &= 1-\xi \\ N^{(1)}_2(\xi , \eta ) &= 1-\eta . \label {eq:formfunc6} \end {align}
These form functions fulfill the property \(N_0^{(n)}+N_1^{(n)}+N_2^{(n)}=1\), which is called the partition of unity.
In the following, we need the derivatives of the shape functions with respect to the positions \(x\) and \(y\). In the general case, we obtain \begin {align} \frac {\partial N_i^{(n)}}{\partial x} &= \frac {\partial N_i^{(n)}}{\partial \xi } \frac {\partial \xi }{\partial x} + \frac {\partial N_i^{(n)}}{\partial \eta } \frac {\partial \eta }{\partial x} \\ \frac {\partial N_i^{(n)}}{\partial y} &= \frac {\partial N_i^{(n)}}{\partial \xi } \frac {\partial \xi }{\partial y} + \frac {\partial N_i^{(n)}}{\partial \eta } \frac {\partial \eta }{\partial y}, \end {align}
or in compact matrix-vector notation \begin {equation} \nabla _{x,y} N_i^{(n)}\cdot \t {J} = \nabla _{\xi ,\eta } N_i^{(n)}, \label {eq:formgrad} \end {equation} where \(\nabla _{x,y}\) denotes the gradient with respect to the displayed coordinates. The matrix \begin {equation} \t {J} = \begin {pmatrix} \partial x/\partial \xi & \partial x/\partial \eta \\ \partial y/\partial \xi & \partial y/\partial \eta \end {pmatrix} = \begin {pmatrix} \Delta x & 0 \\ 0 & \Delta y \end {pmatrix} \label {eq:jacobi} \end {equation} is called the Jacobi matrix. In our example, the explicit matrix on the right-hand side of Eq. \eqref{eq:jacobi} is obtained, which is independent of the box we are looking at. For more complex grids (e.g. Fig. 11.2b), the Jacobi matrix describes the shape of the triangles and thus the structure of the grid. The representation using the rescaled coordinates \(\xi \) and \(\eta \), and thus Eq. \eqref{eq:formgrad} as gradients, decouples the interpolation rule Eq. \eqref{eq:formfunc1}-\eqref{eq:formfunc6} from the structure of the grid and is therefore particularly useful for unstructured grids.
For our grid, we therefore find \begin {align} \frac {\partial N_0^{(0)}}{\partial x} &= -1/\Delta x,\quad \frac {\partial N_0^{(0)}}{\partial y} = -1/\Delta y, \\ \frac {\partial N_1^{(0)}}{\partial x} &= 1/\Delta x,\quad \frac {\partial N_1^{(0)}}{\partial y} = 0, \\ \frac {\partial N_2^{(0)}}{\partial x} &= 0, \frac {\partial N_2^{(0)}}{\partial y} = 1/\Delta y, \\ \frac {\partial N_0^{(1)}}{\partial x} &= 1/\Delta x, \frac {\partial N_0^{(1)}}{\partial y} = 1/\Delta y, \label {eq:N10der} \\ \frac {\partial N_1^{(1)}}{\partial x} &= -1/\Delta x,\quad \frac {\partial N_1^{(1)}}{\partial y} = 0, \\ \frac {\partial N_2^{(1)}}{\partial x} &= 0,\quad \frac {\partial N_2^{(1)}}{\partial y} = -1/\Delta y \label {eq:N12der} \end {align}
for the derivatives of the shape functions. Since we have only used linear elements, these derivatives are all constants.
11.4 Galerkin method
We can now use the Galerkin method to determine the linear system of equations that describes the discretized differential equation. Again, we distinguish between the element matrices and the system matrix. For the element matrix, we write the contribution of the shape function to the Galerkin condition. This yields \begin {equation} \begin {split} (N_I^{(n)}, R) &= \left (N_I^{(n)}, \nabla ^2 \Phi + \frac {\rho (\v {r})}{\varepsilon }\right ) \\ &= \int _{\partial \Omega } \dif ^2r N_I^{(n)} (v{r}) \cdot \hat {n} (v{r}) - \sum _J a_J (N_I^{(n)}, \nabla N_J^{(n)}) + \frac {1}{\varepsilon } (N_I^{(n)}, \rho ), \\ &= - \sum _J K_{IJ}^{(n)} a_J + f_I^{(n)}, \end {split} \end {equation} where \(K_{IJ}^{(n)}\) is now the element matrix and \(f_I^{(n)}\) is the element’s contribution to the right-hand side. We get \begin {equation} K_{IJ}^{(n)} = (\nabla N_I^{(n)}, \nabla N_J^{(n)}). \end {equation} where for two vector fields \(\v {f}(\v {r})\) and \(\v {g}(\v {r})\) the scalar product is defined as \begin {equation} (\v {f}, \v {g}) = \int _\Omega \dif ^3r\, \v {f}^*(\v {r})\cdot \v {g}(\v {r}), \end {equation} i.e. as a Cartesian scalar product between the two function values. The contribution of the element to the right side is \begin {equation} f_I^{(n)} = \frac {1}{\varepsilon }(N_I^{(n)}, \rho ) + \int _{\partial \Omega } \dif ^2r\, N_I^{(n)}(\v {r})\nabla \Phi \cdot \hat {n}(\v {r}). \label {eq:rhs2d} \end {equation}
Example: We now calculate the element matrices for the two elements of our structured example mesh. For example, the component \(I=0\) and \(J=0\) of the element \((0)\) is \begin {equation} \begin {split} K_{00}^{(0)} &= (\nabla N_0^{(0)}, \nabla N_0^{(0)}) \\ &= \int _{\Omega ^{(0)}} \dif ^2r \left ( \frac {1}{\Delta x^2} + \frac {1}{\Delta y^2} \right ) \\ &= \frac {\Delta x\Delta y}{2} \left ( \frac {1}{\Delta x^2} + \frac {1}{\Delta y^2} \right ) \\ &= \frac {1}{2}\left (\frac {\Delta y}{\Delta x} + \frac {\Delta x}{\Delta y}\right ) \end {split} \end {equation} where the factor \(\Delta x\Delta y/2\) is the area of the element. In the following, we consider the special case \(\Delta x=\Delta y\), in which \(K_{00}^{(0)}=1\) is obtained. (In the one-dimensional case, a \(1/\Delta x\) would remain here. The units of \(K\) thus differ in the one-dimensional and two-dimensional case!)
The other scalar products can be calculated similarly. We obtain \begin {equation} \t {K}^{(0)} = \t {K}^{(1)} = \begin {pmatrix} 1 & -1/2 & -1/2 \\ -1/2 & 1/2 & 0 \\ -1/2 & 0 & 1/2 \end {pmatrix} \label {eq:elmat2d} \end {equation} for both element matrices. These matrices are identical because the numbering of the local element nodes was chosen such that the two triangles can be rotated into each other (see Fig.
From these element matrices, we now have to construct the system matrix. The local node indices are shown in Fig. These correspond to the columns and rows of Eq. \eqref{eq:elmat2d}. They must now be mapped to the global node indices and summed in the system matrix. For example, for element \((8)\) in Fig. 11.3a, we have to map the local node \(0\) to the global node \(5\), \(0\to 5\). That is, the first row of the element matrix becomes the sixth row of the system matrix. (It is the sixth row, not the fifth row, because the indexing starts at zero.) Furthermore, we have to map \(1\to 6\) and \(2\to 9\). The contribution \(\Delta \t {K}^{(8)}\) of element \((8)\) to the \(16\times 16\) system matrix is therefore \begin {equation} \Delta \t {K}^{(8)} = \left (\begin {array}{*{16}c} \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & 1 & -\frac {1}{2} & \cdot & \cdot & -\frac {1}{2} & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & -\frac {1}{2} & \frac {1}{2} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & -\frac {1}{2} & \cdot & \cdot & \cdot & \frac {1}{2} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \end {array}\right ) \label {eq:elmat2dlarge} \end {equation} whereby entries with the value \(0\) are shown as a dot (\(\cdot \)) for better visual representation. The total system matrix is then the sum of all elements, \(\t {K}=\sum _n \t {K}^{(n)}\). We get \begin {equation} \t {K} = \left (\begin {array}{*{16}c} 1 & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \bar {\frac {1}{2}} & 1 & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & 2 & \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & 2 & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & 2 & \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & 2 & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & 1 & \bar {\frac {1}{2}} & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} \\ \cdot & \cdot & \cdot & \cdot & \cdot \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {\frac {1}{2}} & 1 \end {array}\right ) \label {eq:sysmat2d} \end {equation} where the bar above the number indicates a minus, e.g. \(\bar {1}=-1\). This \(16\times 16\) matrix is again not regular; its rank is 15. This means that at least one Dirichlet boundary condition is needed to obtain a solvable problem. This example also shows that the system matrix is difficult to calculate by hand and that we need a computer to help us.
11.5 Boundary conditions
11.5.1 Dirichlet boundary conditions
Dirichlet boundary conditions work analogously in higher dimensions to the one-dimensional case. We fix the function value at a node. We obtain \(\Phi _N(\v {r}_n)=a_n\equiv \Phi _n\), where \(\Phi _n\) is the chosen function value, and thus replace a Galerkin condition by fixing the potential at the node.
11.5.2 Neumann boundary conditions
As in the one-dimensional case, Neumann boundary conditions are incorporated into the right-hand side via the surface term in Eq. These conditions are therefore defined on the sides of the triangles. For a constant directional derivative \(\Phi ^\prime = \nabla \Phi \cdot \hat {n}\), we obtain \begin {equation} f_I 2D = \frac {1}{\varepsilon } (N_I 2D, \rho ) + \Phi ' \int _{\partial \Omega } \dif r N_I 2D (v{r}). \label {eq:rhs2d2} \end {equation} The integral in Eq. \eqref{eq:rhs2d2} is carried out over the side of the triangle. For the side between nodes \(2\) and \(3\) (see Fig. 11.3), for example, the shape functions \(N_0^{(0)}\) and \(N_1^{(0)}\) (element \((4)\)) are not equal to zero. We obtain \begin {align} f_0^{(4)} &= \frac {1}{\varepsilon }(N_0^{(0)}, \rho ) + \Phi ^\prime \int _0^{\Delta x} \dif x\, (1-x/\Delta x) = \frac {1}{\varepsilon }(N_0^{(0)}, \rho ) + \frac {1}{2}\Phi ^\prime \Delta x \\ f_1^{(4)} &= \frac {1}{\varepsilon }(N_1^{(0)}, \rho ) + \Phi ^\prime \int _0^{\Delta x} \dif x\, x/\Delta x = \frac {1}{\varepsilon }(N_1^{(0)}, \rho ) + \frac {1}{2}\Phi ^\prime \Delta x \end {align}
for the right-hand side. The boundary conditions, which are obtained without further modification of the right-hand side (see Eq. \eqref{eq:sysmat2d}), are therefore Neumann conditions with a vanishing derivative, \(\Phi ^\prime = 0\).