Kapitel 3
Transporttheorie
Kontext: Dieses Lernmodul führt die Grundlagen des Modellproblems ein, welches wir im Laufe der Lehrveranstaltung mit numerischen Methoden lösen werden. Hier geht es zunächst um die Grundlagen der Transporttheorie.
3.1 Diffusion und Drift
Diffusiver Transport ist einfach zugänglich über das Bild des “Random Walk”, einer zufälligen stochastischen Bewegung von Teilchen. Solche zufälligen Bewegungsprozesse wurden zuerst von dem Botaniker Robert Brown (1773-1858) beschrieben und tragen den Namen Brownsche Bewegung oder Brownsche Molekularbewegung. Robert Brown wusste damals allerdings nicht von Molekülen und dachte zu seinen Lebzeiten, dass diese Bewegung auf aktive Prozesse (der “Lebenskraft” der Pollen) zurückzuführen sei. Heute wissen wir, dass diese Bewegung durch thermische Fluktuationen verursacht wird, also Moleküle die zufällig auf die Pollen treffen und diese in eine Richtung stoßen. Diese Erklärung benötigt die Existenz von Atomen und wurde erst 1905 von Albert Einstein (Einstein, 1905) hoffähig gemacht.
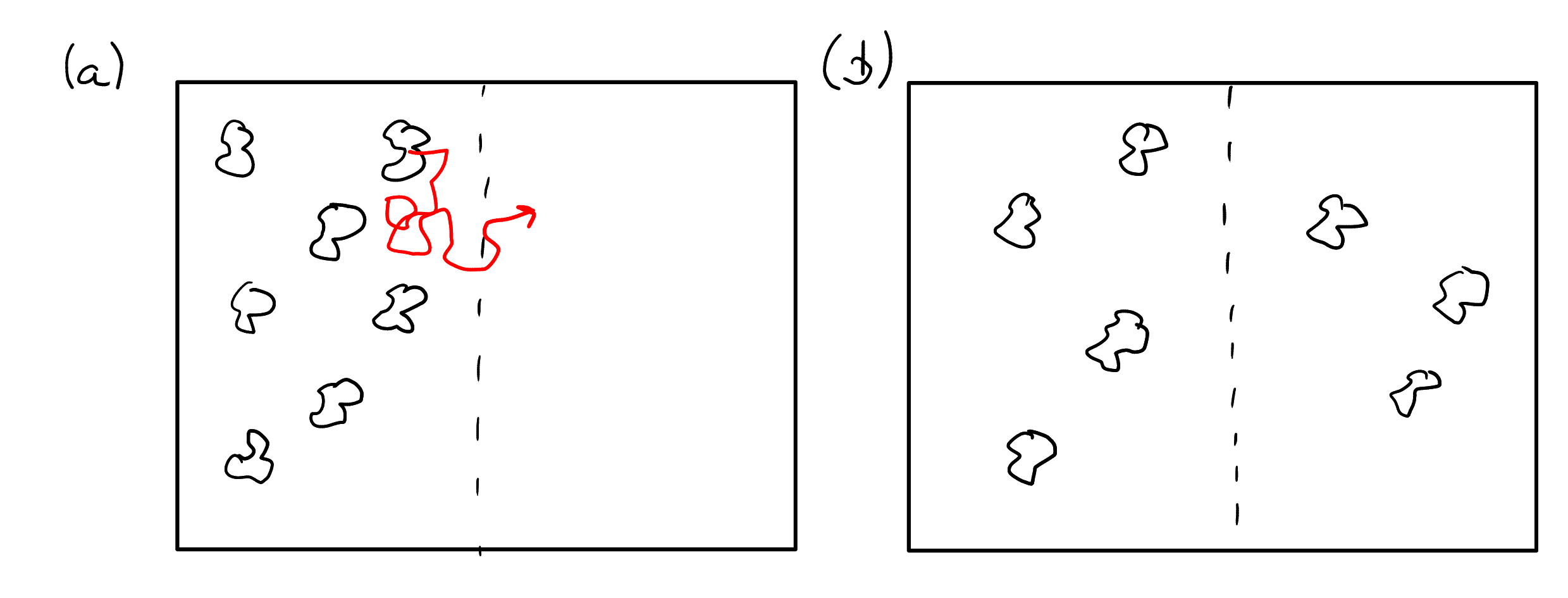
Brownsche Molekularbewegung führt zu diffusivem Transport. Abbildung 3.1 zeigt ein einfaches qualitatives Gedankenexperiment. Die Konfiguration in Abb. 3.1a zeigt eine Lokalisierung der “Pollen” in der linken Hälfte der gezeigten Domäne. Durch deren zufällige Bewegung (als Beispiel gezeigt an der roten Linie in Abb. 3.1a) werden einige der Pollen die gestrichelte Grenzlinie in die rechte Hälfte überschreiten und auch wieder zurück kommen. Nach einer gewissen Zeit lässt sich der Anfangszustand nicht mehr identifizieren und die Pollen verteilen sich in der gesamten Domäne (Abb. 3.1b). Die Konzentration ist nun konstant. Die Pollen bewegen sich zwar weiter, aber in Mittel bewegt sich die gleiche Zahl Pollen nach links wie nach rechts. Im Fall der in Abb. 3.1a gezeigt ist, ist diese Symmetrie gebrochen.
Dieses Gedankenexperiment kann einfach mathematisch formalisiert werden. Wir betrachten ein Teilchen, das eine Zufallsbewegung in einer Dimension vollführt. Wir beginnen mit einem Teilchen, das zufällig auf einer Geraden hin- und herspringt. Die Gerade liege entlang der x-Richtung. Das Teilchen kann nur zu vorher festgelegten Positionen auf der x-Achse springen, die wir mit \(x_j\) bezeichnen und die äquidistant verteilt seien, \(x_j-x_{j-1}=\Delta x\) für \(j\in \mathbb {Z}\) (siehe Abb. 3.2).
Ein Teilchen springe mit einer Wahrscheinlichkeit \(p\) nach links und mit einer Wahrscheinlichkeit \(q\) nach rechts. Darüberhinaus haben wir die Wahrscheinlichkeit überhaupt ein Teilchen zur Zeit \(t\) bei Position \(x\) zu finden. Diese ist auf dem 1D Gitter durch die Funktion \(P(x,t)\) gegeben.
3.1.1 Diffusion
Wir betrachten zunächst den Fall \(p=q=1/2\), also dass die Wahrscheinlichkeiten für die Sprünge nach links und rechts identisch sind. Wir nehmen an, das Teilchen springe von einem Platz zum benachbarten in einem diskreten, endlichen und konstanten Zeitschritt \(\tau \). Dann ist die Wahrscheinlichkeit ein Teilchen zur Zeit \(t+\tau \) am Ort \(x\) zu finden, wenn zur Zeit \(t\) mit einer Wahrscheinlichkeit \(P(x-\Delta x,t)\) ein Teilchen bei der Position \(x-\Delta x\) zu finden war und mit der Wahrscheinlichkeit \(P(x+\Delta x,t)\) eines bei \(x+\Delta x\), gegeben durch \begin {equation} P(x,t+\tau )=\frac {1}{2}P(x+\Delta x,t)+\frac {1}{2}P(x-\Delta x,t). \end {equation} Indem wir \(P(x,t)\) auf beiden Seiten abziehen und durch \(\tau \) teilen, erhalten wir die folgende äquivalente Form: \begin {equation} \frac {P(x,t+\tau )-P(x,t)}{\tau } = \frac {\Delta x^2}{2\tau }\frac {P(x+\Delta x,t)-2P(x,t)+P(x-\Delta x,t)}{\Delta x^2} \end {equation} Wir können nun den Grenzübergang zum “Kontinuum” machen. Für \(\tau \rightarrow 0\) und gleichzeitig \(h\rightarrow 0\) unter der Bedingung, dass \begin {equation} \lim _{\Delta x\rightarrow 0, \tau \rightarrow 0}\frac {\Delta x^2}{2\tau }=D \end {equation} erhält man \begin {equation} \frac {\partial P(x,t)}{\partial t}=D\frac {\partial ^2 P(x,t)}{\partial x^2}. \end {equation} Dies die wohlbekannte Diffusionsgleichung. In mehreren Dimensionen wird aus der zweiten Ableitung der Laplace-Operator \(\nabla ^2\), \begin {equation} \frac {\partial P(x,t)}{\partial t}=D \nabla ^2 P(x,t). \label {eq:diffusion} \end {equation} Diese Gleichung ist nur dann korrekt, wenn die Diffusionskonstante auch wirklich konstant ist und nicht räumlich variiert.
3.1.2 Drift
Wie sieht es aus, wenn die Wahrscheinlichkeiten für die Sprünge nach rechts oder links nicht gleich sind, \(p\ne q\) (aber natürlich \(p+q=1\))? Wir gehen nach wie vor von diskreten, gleichförmigen Zeitschritten und äquidistanten Stützstellen aus.
In diesem Fall haben wir \begin {equation} P(x,t+\tau )=pP(x+\Delta x,t)+qP(x-\Delta x,t) \end {equation} und somit folgt \begin {equation} \frac {P(x,t+\tau )-P(x,t)}{\tau }=\frac {\Delta x^2}{\tau }\frac {pP(x+\Delta x,t)-P(x,t)+qP(x-\Delta x,t)}{\Delta x^2}. \label {eq:driftpq} \end {equation} Wir schreiben \begin {equation} p=\frac {1}{2}-\varepsilon \quad \text {und}\quad q=\frac {1}{2}+\varepsilon \quad \text {mit}\quad 0\le |\varepsilon |\le \frac {1}{2} \quad \text {oder}\quad 2\varepsilon = q-p, \end {equation} wobei \(\varepsilon \) nun angibt, um wieviel wahrscheinlicher ein Sprung nach rechts als nach links ist. Ein positives \(\varepsilon \) heißt also, dass die Partikel sich im Mittel nach rechts bewegen werden – dies ist die Driftbewegung. Wir können nun Gl. \eqref{eq:driftpq} mit Hilfe von \(\varepsilon \) als \begin {equation} \begin {split} \frac {P(x,t+\tau )-P(x,t)}{\tau }=& \frac {\Delta x^2}{2\tau }\frac {P(x+\Delta x,t)-2P(x,t)+P(x-\Delta x,t)}{\Delta x^2}\\ &-\frac {2\varepsilon \Delta x}{\tau }\frac {P(x+\Delta x,t)-P(x-\Delta x,t)}{2\Delta x} \end {split} \end {equation} ausdrücken. In den Grenzfällen \(\tau \rightarrow 0\) und \(\Delta x\rightarrow 0\) fordern wir \begin {equation} \lim _{\Delta x\rightarrow 0, \tau \rightarrow 0}\frac {\Delta x^2}{2\tau }=D \quad \text { und }\quad \lim _{\Delta x\rightarrow 0, \tau \rightarrow 0}\frac {2\varepsilon \Delta x}{\tau }=v \label {eq:limit2} \end {equation} und erhalten somit die Drift-Diffusions-Gleichung \begin {equation} \frac {\partial P(x,t)}{\partial t}=\left (D\frac {\partial ^2}{\partial x^2} -v\frac {\partial }{\partial x}\right ) P(x,t). \label {eq:driftdiffusion} \end {equation} Hier beschreibt der erste Summand auf der rechten Seite wieder den Diffusionsprozess. Der zweite Summand ist ein Driftprozess und \(v\) eine konstante Driftgeschwindigkeit. (Aus Gl. \eqref{eq:limit2} und \eqref{eq:driftdiffusion} wird ersichtlich, dass die Einheit von \(v\) genau einer Geschwindigkeit entspricht.) Es ist die Geschwindigkeit mit der sich das Teilchen (im Mittel) entlang der \(x\)-Achse bewegen. Die Lösung dieser Gleichung wurde bereits im vorhergehenden Kapitel besprochen. Aus der Lösung des vorhergehenden Kapitels wird auch klar, dass die Driftbewegung für positive \(v\) in Richtung der positiven \(x\)-Achse ist. Dies ist konsistent mit der obigen Definition von \(\varepsilon \).
Anmerkung: Die Bewegung unseres Teilchen wurde mit Hilfe einer Aufenthaltswahrscheinlichkeit \(P\) modelliert. Im thermodynamischen Limes, also für ganz viele Teilchen (üblicherweise in Größenordnung der Avogadroschen Zahl \(N_A\)), wird aus dieser Wahrscheinlich die Dichte \(\rho \) oder die Konzentration \(c\). Man kann also einfach in den oben genannten Gleichungen die Wahrscheinlichkeit \(P\) durch eine Teilchenkonzentration \(c\) ersetzen. Der Grund hierfür ist, dass wir die Teilchenkonzentration als Ensemble-Mittel schreiben können, \begin {equation} c(x, t) = \langle 1 \rangle (x, t), \end {equation} wobei der Mittelwert \begin {equation} \langle f(x) \rangle (x, t) = f(x) P(x, t). \end {equation}
3.2 Kontinuität
Die Gleichungen \eqref{eq:diffusion} und \eqref{eq:driftdiffusion} vermischen zwei Konzepte, die wir hier jetzt getrennt behandeln wollen: Die Erhaltung der Anzahl der Teilchen (Kontinuität) und der Prozess, welcher zu einem Teilchenstrom führt (Diffusion oder Drift). Die Teilchenzahl ist einfach deshalb erhalten, weil wir keine Atome aus dem Nichts erzeugen oder in das Nichts vernichten können. Wir wissen also, wenn wir eine gewissen Anzahl Teilchen \(N_{\text {tot}}\) in unserem Gesamtsystem haben, dass diese Anzahl \begin {equation} N_{\text {tot}} = \int \dif ^3r \, c(\v {r}) \end {equation} sich nicht über die Zeit ändern kann: \(\dif N_{\text {tot}}/\dif t=0\).
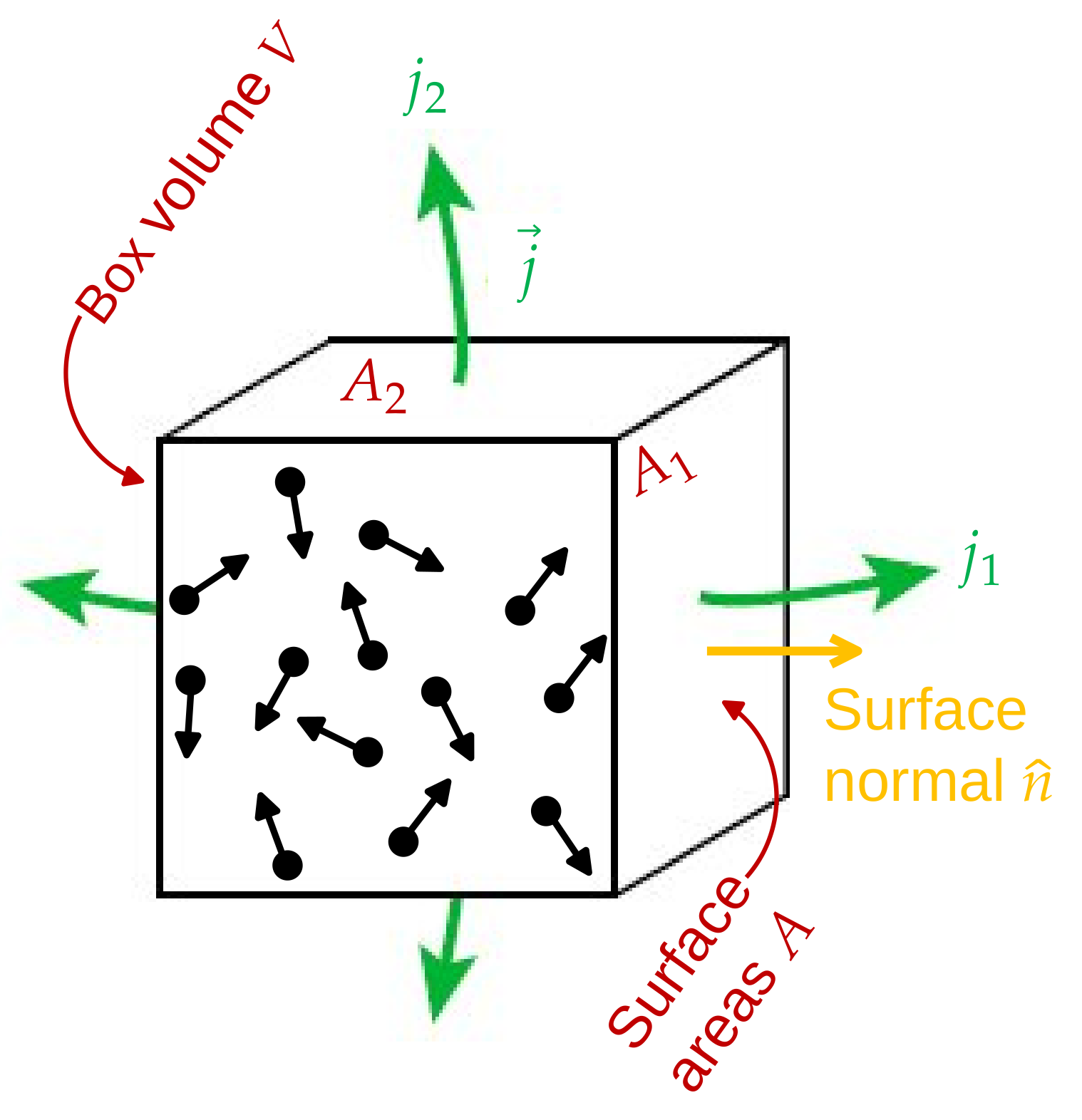
Für einen kleinen Ausschnitt mit Volumen \(V\) aus diesem Gesamtvolumen kann sich die Teilchenzahl ändern, weil diese über die Wände des Probevolumens fließen können (siehe Abb. 3.3). Die Änderung dieser Teilchenzahl ist zum einen gegeben durch \begin {equation} \dot {N} = \frac {\partial }{\partial t} \int _V \dif ^3r \, c(\v {r}, t) = \int _V \dif ^3r \, \frac {\partial c}{\partial t}. \label {eq:nchange} \end {equation} Die Änderung \(\dot {N}\) muss aber auch durch die Anzahl der Partikel, die über die Seitenwände abfließen, gegeben sein. Für einen Würfel (Abb. 3.3) mit sechs Wänden gilt \begin {equation} \begin {split} \dot {N} = & - j_{\text {rechts}} A_{\text {rechts}} - j_{\text {links}} A_{\text {links}} \\ & - j_{\text {oben}} A_{\text {oben}} - j_{\text {unten}} A_{\text {unten}} \\ & - j_{\text {vorne}} A_{\text {vorne}} - j_{\text {hinten}} A_{\text {hinten}} \end {split} \label {eq:dotN} \end {equation} wenn die Wände klein genug sind, so dass \(j\) nahezu konstant über \(A\) ist. (Die Stromdichte \(j\) hat die Einheit Anzahl Partikel/Zeit/Fläche.)
Hier bezeichnet der skalare Strom \(j\) den Strom, der aus der Fläche heraus fließt. Für eine allgemeine vektorielle Stromdichte \(\v {j}\), welche die Stärke und Richtung des Teilchenstroms angibt, ist \(j_i = \v {j}_i \cdot \hat {n}_i\) wobei \(\hat {n}_i\) der Normalenvektor auf die Wand \(i\) ist. Der Strom durch die Wand ist also nur die Komponente von \(\v {j}\), die parallel zur Oberflächennormale steht. Mit diesem Argument können wir die Änderung der Teilchenzahl allgemein als \begin {equation} \dot {N} = -\int _{\partial V} \dif ^2r \, \v {j}(\v {r})\cdot \hat {n}(\v {r}) \label {eq:flux} \end {equation} ausdrücken, wobei \(\partial V\) die Oberfläche des Volumens \(V\) bezeichnet. In dieser Gleichung ist explizit angezeigt, dass selbstverständlich sowohl der Fluss \(\v {j}\) als auch die Oberflächennormale \(\hat {n}\) von der Position \(\v {r}\) auf der Oberfläche abhängen.
Alternativ können wir auch die Änderung der Teilchenzahl Gl. \eqref{eq:dotN} folgendermaßen gruppieren: \begin {equation} \begin {split} \dot {N} = & - (j_{\text {rechts}} + j_{\text {links}}) A_{\text {rechts/links}} \\ & - (j_{\text {oben}} + j_{\text {unten}}) A_{\text {oben/unten}} \\ & - (j_{\text {vorne}} + j_{\text {hinten}}) A_{\text {vorne/hinten}} \end {split} \end {equation} Hierbei haben wir die Tatsache genutzt, dass \(A_{\text {rechts}}=A_{\text {links}}\equiv A_{\text {rechts/links}}\). Nun ist aber \begin {equation} \begin {split} j_{\text {rechts}} &= \hat {x} \cdot \v {j}(x+\Delta x/2,y,z) = j_x(x+\Delta x/2,y,z) \quad \text {und} \\ j_{\text {links}} &= -\hat {x} \cdot \v {j}(x-\Delta x/2,y,z) = -j_x(x-\Delta x/2,y,z) \end {split} \end {equation} da \(\hat {n}=\hat {x}\) für die rechte Wand aber \(\hat {n}=-\hat {x}\) für die linke Wand. Hierbei ist \(\hat {x}\) der Normalenvektor entlang der \(x\)-Achse des Koordinatensystems. Es dreht sich also zwischen der rechten und linken Fläche das Vorzeichen der Oberflächennormale um. Das gleiche gilt für die Wände oben/unten und vorne/hinten. Wir können diese Gleichung weiterhin umschreiben als \begin {equation} \begin {split} \dot {N} = & - \frac {j_x(x+\Delta x/2,y,z) - j_x(x-\Delta x/2,y,z)}{\Delta x} V \\ & - \frac {j_y(x,y+\Delta y/2,z) - j_y(x,y-\Delta y/2,z)}{\Delta y} V \\ & - \frac {j_z(x,y,z+\Delta z/2) - j_z(x,y,z-\Delta z/2)}{\Delta z} V, \end {split} \label {eq:dotNdiscr} \end {equation} da \(V=A_{\text {rechts/links}}\Delta x=A_{\text {oben/unten}}\Delta y=A_{\text {vorne/hinten}}\Delta z\). Die Faktoren vor dem Volumen \(V\) in Gl. \eqref{eq:dotNdiscr} sind nun aber genau der Differenzenquotienten der Flüsse \(j_i\), jeweils in die \(x\)-, \(y\)- und \(z\)-Richtung. Für kleine Volumina (und kleine \(\Delta x\), etc.) wird dies zu \begin {equation} \dot {N} = -\int _{V} \dif ^3r \, \nabla \cdot \v {j}(\v {r}). \label {eq:flux2} \end {equation} Wir habe hier gerade heuristisch den Gaussschen Satz (engl. “Divergence Theorem” - siehe auch Gl. \eqref{eq:divergencetheorem}) hergeleitet, um Gl. \eqref{eq:flux} als Volumenintegral auszudrücken.
Anmerkung: Der Gausssche Satz ist ein wichtiges Ergebnis der Vektoranalysis. Er wandelt ein Integral über ein Volumen \(V\) in ein Integral über die Oberfläche \(\partial V\) dieses Volumens um. Für ein Vektorfeld \(\v {f}(\v {r})\) gilt: \begin {equation} \int _V \dif ^3 r\, \nabla \cdot \v {f}(\v {r}) = \int _{\partial V} \dif ^2 r\, \v {f}(\v {r}) \cdot \hat {n}(\v {r}) \label {eq:divergencetheorem} \end {equation} Hier ist \(\hat {n}(\v {r})\) der Normalenvektor, welcher auf dem Rand \(\partial V\) des Volumens \(V\) nach außen zeigt.
Gleichung \eqref{eq:nchange} und \eqref{eq:flux2} zusammen ergeben \begin {equation} \int _V \dif ^3r \, \left \{\frac {\partial c}{\partial t}+\nabla \cdot \v {j}\right \} = 0. \label {eq:continuityweak} \end {equation} Da dies für jedes beliebige Volumen \(V\) gilt, muss auch \begin {equation} \frac {\partial c}{\partial t}+\nabla \cdot \v {j} = 0 \label {eq:continuity} \end {equation} erfüllt sein. Diese Gleichung trägt den Namen Kontinuitätsgleichung. Sie beschreibt die Erhaltung der Teilchenzahl bzw. der Masse des Systems.
Anmerkung: In der hier dargestellten Herleitung haben wir implizit bereits die starke Formulierung und eine schwache Formulierung (engl. “weak formulation” einer Differentialgleichung kennengelernt. Gleichung \eqref{eq:continuity} ist die starke Formulierung der Kontinuitätsgleichung. Diese verlangt, dass die Differentialgleichung für jeden räumlichen Punkt \(\v {r}\) erfüllt ist. Die entsprechende schwache Formulierung ist Gl. \eqref{eq:continuityweak}. Hier wird nur verlangt, dass die Gleichung in einer Art Mittelwert, hier als Integral über ein Probevolumen \(V\), erfüllt ist. Innerhalb des Volumens muss die starke Form nicht erfüllt sein, aber das Integral über diese Abweichungen (die wir später als “Residuum” bezeichnen werden) muss verschwinden. Die schwache Formulierung ist für endliche Probevolumina \(V\) damit eine Näherung. In der Methode der finiten Elemente löst man eine schwache Gleichung für eine gewissen (approximative) Ansatzfunktion exakt. Die schwache Formulierung wird daher im Verlauf dieser Veranstaltung wichtig werden.
Wir können weiterhin noch verlangen, dass innerhalb unseres Probevolumens “Teilchen” produziert werden. In der aktuellen Interpretation der Gleichung wären dies z.B. chemische Reaktionen, die einen Teilchentyp in einen anderen umwandeln. Eine identische Gleichung gilt für den Wärmetransport. Hier wäre ein Quellterm die Produktion von Wärme, z.B. durch ein Heizelement. Gegeben ein Quellenstrom \(Q\) (mit Einheit Anzahl Partikel/Zeit/Volumen), kann die Kontinuitätsgleichung auf \begin {equation} \frac {\partial c}{\partial t}+\nabla \cdot \v {j} = Q \label {eq:continuitywithsource} \end {equation} erweitert werden. Die Kontinuitätsgleichung mit Quellterm wird auch manchmal als Bilanzgleichung bezeichnet.
Anmerkung: Gleichung \eqref{eq:continuitywithsource} beschreibt die zeitliche Veränderung der Konzentration \(c\). Eine verwandte Frage ist die nach der Lösung dieser Gleichung nach sehr langer Zeit - wenn sich ein dynamisches Gleichgewicht eingestellt hat. Dieses Gleichgewicht ist dadurch gekennzeichnet, dass \(\partial c/\partial t=0\). Die Gleichung \begin {equation} \nabla \cdot \v {j} = Q \end {equation} ist die stationäre Variante der Kontinuitätsgleichung.
3.2.1 Drift
Kommen wir zurück zu Transportprozessen, zunächst zu Drift. Wenn sich alle Teilchen in unserem Probevolumen in mit der Geschwindigkeit \(\v {v}\) bewegen, dann führt das zu einem Teilchenstrom \begin {equation} \v {j}_{\text {Drift}} = c \v {v}. \label {eq:drift} \end {equation} Eingesetzt in die Kontinuitätsgleichung \eqref{eq:continuity} ergibt dies den Drift-Beitrag zur Drift-Diffusions-Gleichung \eqref{eq:driftdiffusion}.
3.2.2 Diffusion
Aus unserem obigen Gedankenexperiment wird klar, dass der Diffusionstrom immer in Richtung der niedrigen Konzentration, also in entgegengesetzte Richtung des Gradienten \(\nabla c\) der Konzentration, gehen muss. Der entsprechende Strom ist gegeben durch \begin {equation} \v {j}_{\text {Diffusion}} = - D \nabla c. \label {eq:stationary} \end {equation} Eingesetzt in die Kontinuitätsgleichung \eqref{eq:continuity} ergibt dies die Diffusionsgleichung \eqref{eq:diffusion}.
Die gesamte Drift-Diffusionsgleichung hat daher die Form \begin {equation} \frac {\partial c}{\partial t} + \nabla \cdot \left \{-D\nabla c + c\v {v}\right \}=0. \label {eq:drift-diffusion-full} \end {equation} Im Gegensatz zu Gleichungen \eqref{eq:diffusion} und \eqref{eq:driftdiffusion} gilt diese Gleichung auch wenn die Diffusionskonstante \(D\) oder Drift-Geschwindigkeit \(\v {v}\) räumlich variiert.
Anmerkung: Wir haben hier die Transporttheorie im Sinne einer Teilchenkonzentration \(c\) eingeführt. Die Kontinuitätsgleichung beschreibt jedoch allgemein die Erhaltung einer bestimmten Größe, in unserem Fall der Teilchenzahl (oder äquivalent der Masse). Andere physikalisch erhaltene Größen sind der Impuls und die Energie. Die Kontinuitätsgleichung für den Impuls führt zur Navier-Stokes Gleichung. Die Kontinuitätsgleichung für die Energie führt zur Wärmeleitungsgleichung. Für das Beispiel dieser Veranstaltung ist nur die Erhaltung der Masse relevant.
Literaturverzeichnis
A. Einstein. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys., 17:549, 1905.