Kapitel 10
Finite Elemente in mehreren Dimensionen
Kontext: Wir verallgemeinern nun die Ergebnisse des vorhergehenden Kapitels auf mehrere Dimensionen. Dies hat mehrere technische Hürden: Für die partielle Integration müssen wir nun Ergebnisse der Vektoranalysis, insbesondere den Gaussschen Satz bzw. die Greenschen Formeln nutzen. Die Diskretisierung erfolgt in Form von Elementen, üblicherweise Dreiecke oder Tetraeder. Durch diese komplexere Geometrie der Elemente wird eine saubere Buchhaltung der Indices, also die Unterscheidung von globalen Knoten, Elementknoten und Elementen wichtig.
10.1 Differenzierbarkeit
Zur Illustration, wie die Anforderung an die Differenzierbarkeit in höherdimensionalen Problemen reduziert werden kann, und wir damit wieder lineare Basisfunktionen verwenden können, wird hier weiter die Poisson-Gleichung betrachtet. In \(D\)-Dimensionen (mit üblicherweise \(D=2\) oder \(D=3\)) führt die Poisson-Gleichung zu dem Residuum \begin {equation} R(\v {r}) = \nabla ^2 \Phi + \frac {\rho (\v {r})}{\varepsilon } = \nabla \cdot \left (\nabla \Phi \right ) + \frac {\rho (\v {r})}{\varepsilon } \label {eq:poissonreshighd} \end {equation} wobei \(\v {r}=(x,y,z,\ldots )\) nun ein \(D\)-dimensionaler Vektor ist, der die Position bezeichnet, und \(\nabla ^2\) der Laplace-Operator in \(D\)-Dimensionen. Das Potential \(\Phi (\v {r})\) hängt nun selbstverständlich auch von der räumlichen Position \(\v {r}\) ab. Die rechte Seite von Gl. \eqref{eq:poissonreshighd} ist explizit so geschrieben, dass man die Verknüpfung aus Divergenz und Gradient erkennt, die den Laplace-Operator ergibt.
Wir schreiben nun das gewichtete Residuum auf. Das Skalarprodukt mit einer Testfunktion \(v(\v {r})\) ergibt \begin {align} (v(\v {r}), R(\v {r})) =& \int _\Omega \dif ^Dr\, v(\v {r}) \left ( \nabla ^2 \Phi + \frac {\rho (\v {r})}{\varepsilon } \right ) \\ =& \int _{\partial \Omega } \dif ^{D-1} r\, v(\v {r}) \left (\nabla \Phi \cdot \hat {n}(\v {r})\right ) -\int _\Omega \dif ^Dr\, \nabla v \cdot \nabla \Phi + \int _\Omega \dif ^Dr\, \frac {v(\v {r})\rho (\v {r})}{\varepsilon }, \label {eq:weakformhighd} \end {align}
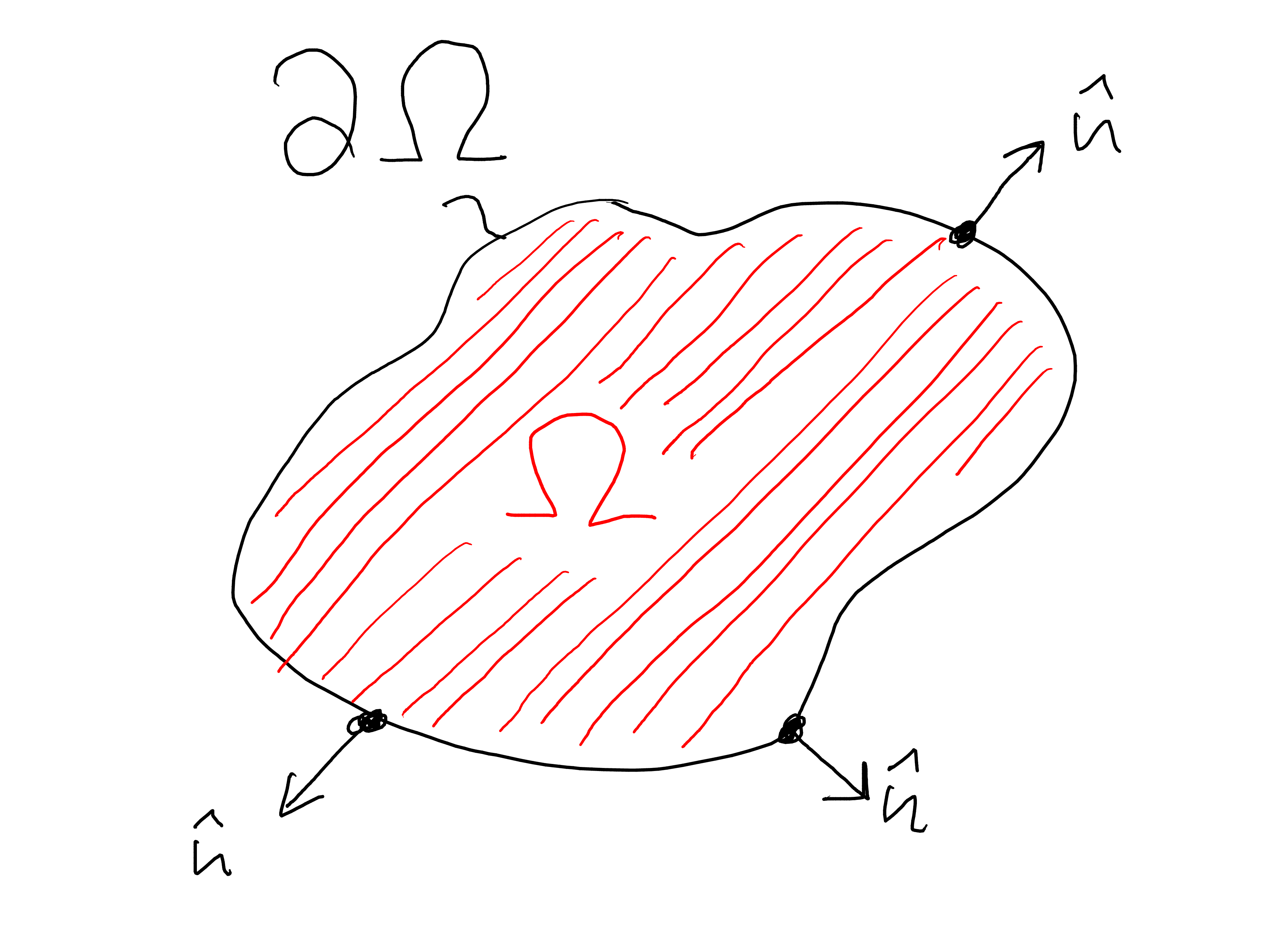
wobei nun die erste Greensche Formel verwandt wurde, um das Flächen- bzw. Volumenintegral über \(\Omega \) umzuschreiben und dabei den Gradienten auf die Testfunktion zu überführen. Die Greensche Formel nimmt hier die Rolle ein, die in dem eindimensionalen Fall die partielle Integration hatte. \(\hat {n}(\v {r})\) ist der Normalenvektor, welcher auf dem Rand \(\partial \Omega \) der Domäne nach außen zeigt (siehe Abb. 10.1. Der erste Term auf der rechten Seite von Gl. \eqref{eq:weakformhighd} wird wieder wichtig werden, wenn wir Neumann-Randbedingungen auf den Rand \(\partial \Omega \) der Domäne vorgeben möchten. Im Dirichlet-Fall verschwindet dieser Term.
Anmerkung: Die Greenschen Formeln sind ein weiteres wichtiges Ergebnis der Vektoranalysis. Sie gehen aus dem Gausschen Satz hervor. Der Gausssche Satz lautet \begin {equation} \int _\Omega \dif ^D r\, \nabla \cdot \v {f}(\v {r}) = \int _{\partial \Omega } \dif ^{D-1} r\, \v {f}(\v {r}) \cdot \hat {n}(\v {r}) \end {equation} wobei \(\partial \Omega \) den \(D-1\) dimensionalen Rand des \(D\)-dimensionalen Integrationsgebiets \(\Omega \) bezeichnet. Weiterhin ist \(\hat {n}(\v {r})\) der Normalenvektor, der senkrecht auf den Rand steht und aus dem Integrationsgebiet hinaus zeigt (siehe auch Abb. 10.1). Wir wenden den Gausschen Satz jetzt auf ein Vektorfeld \(\v {f}(\v {r})=\phi (\v {r})\v {v}(\v {r})\) an, wobei \(\phi (\v {r})\) ein skalares Feld und \(\v {v}(\v {r})\) wiederum ein Vektorfeld ist. Man erhält \begin {equation} \int _\Omega \dif ^D r\, \nabla \cdot \left (\phi \v {v}\right ) = \int _{\partial \Omega } \dif ^{D-1} r\, \left (\phi \v {v}\right ) \cdot \hat {n}. \end {equation} Auf Grund der Kettenregel der Ableitung gilt \begin {equation} \nabla \cdot \left (\phi \v {v}\right ) = \left (\nabla \phi \right )\cdot \v {v} + \phi \left (\nabla \cdot \v {v}\right ). \label {eq:chainrulevec} \end {equation} (Das Gl. \eqref{eq:chainrulevec} gilt sieht man am einfachsten, wenn man sie komponentenweise hinschreibt.) Dies führt zu \begin {equation} \int _\Omega \dif ^D r\, \left (\nabla \phi \cdot \v {v} + \phi \nabla \cdot \v {v}\right ) = \int _{\partial \Omega } \dif ^{D-1} r\, \left (\phi \v {v}\right ) \cdot \hat {n}. \end {equation} Mit \(\v {v}(\v {r})=\nabla \psi \) erhält man die übliche Darstellung der ersten Greenschen Formel, \begin {equation} \int _\Omega \dif ^D r\, \left (\nabla \phi \cdot \nabla \psi + \phi (\v {r}) \nabla ^2\psi \right ) = \int _{\partial \Omega } \dif ^{D-1} r\, \left (\phi \nabla \psi \right ) \cdot \hat {n}. \end {equation}
In Gl. \eqref{eq:weakformhighd} ist nun die Anforderung an die Differenzierbarkeit reduziert. Der Laplace-Operator, also die zweite Ableitung, taucht nicht mehr in dieser Gleichung auf. Wir müssen lediglich Gradienten der Testfunktion \(v(\v {r})\) und des Potentials \(\Phi (\v {r})\) berechnen können.
10.2 Gitter
Wir müssen nun geeignete Basisfunktionen wählen, um mit Hilfe der Galerkin-Bedingungen ein lineares Gleichungssystem zu erhalten. Hierbei ist es nützlich, die Formulierung im Sinne von Formfunktionen und nicht von Basisfunktionen vorzunehmen. Die weitere Entwicklung der Theorie in diesem Kapitel wird für zweidimensionale Probleme (\(D=2\)) vorgenommen.
10.2.1 Triangulierung
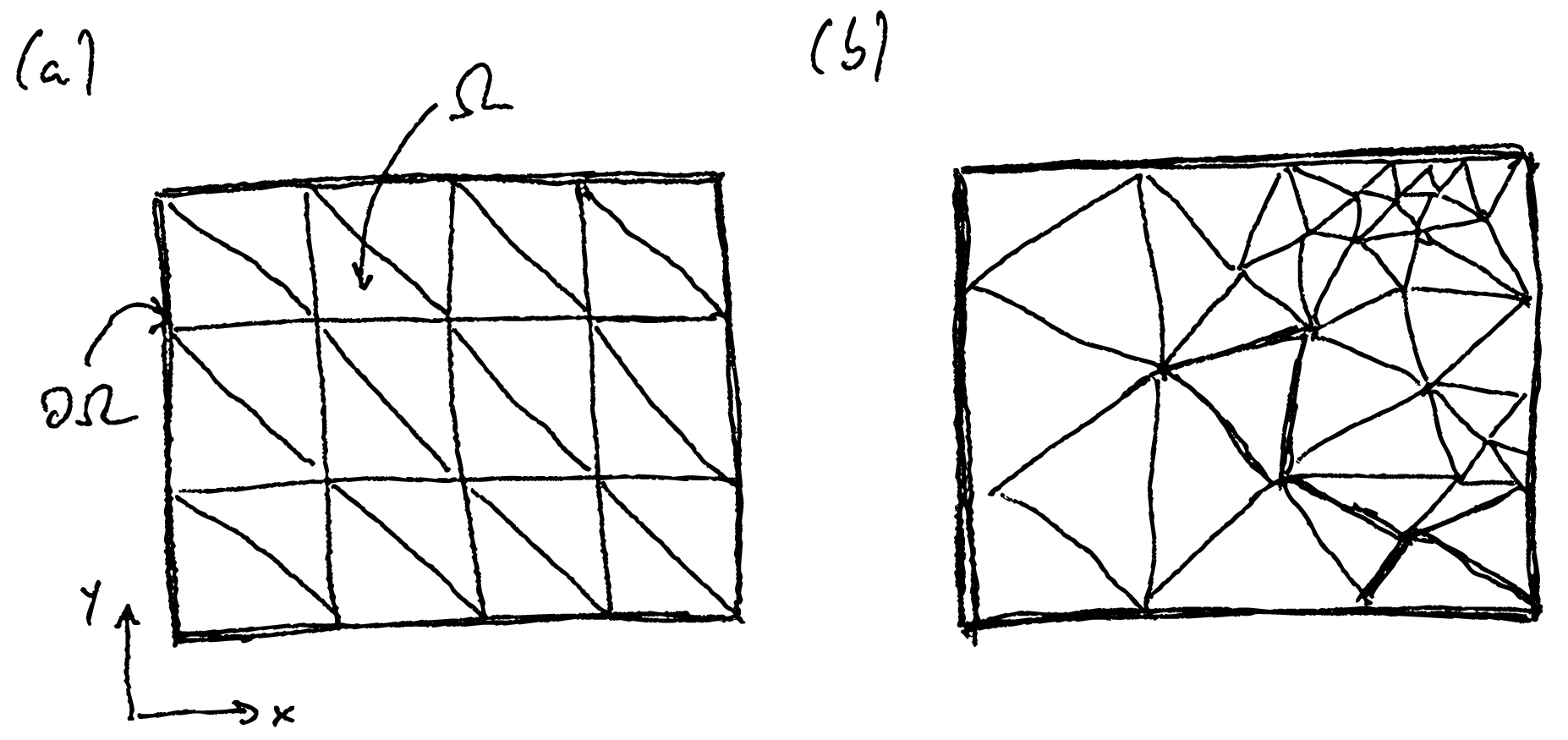
Bevor wir über diese Details der Basisfunktionen reden können, müssen wir die Zerlegung des Simulationsgebiet in Elemente diskutieren. In zwei Dimensionen sind diese Elemente üblicherweise (aber nicht zwingend) Dreiecke, d.h. man nimmt eine Triangulierung des Gebiets vor. Abbildung 10.2 zeigt eine solche Triangulierung für ein rechteckiges (2-dimensionales) Gebiet. Diese Zerlegung nennt man auch das Gitter (oder Netz, engl. “grid” oder “mesh”), die einzelnen Dreiecke Elemente (engl. “elements”) und die Ecken der Dreiecke Knoten (engl “nodes”). Der Prozess der Zerlegung des Gebiets wird Vernetzung genannt. Wir werden hier ausschließlich mit strukturierten Gittern, wie in Abb. 10.2a dargestellt, arbeiten. Viele Simulationspakete unterstützen auch unstrukturierte Gitter wie in Abb. 10.2b gezeigt.
Auch für diese Art der Zerlegung kann man die Zielfunktion \(\Phi (\v {r})\) durch eine Summe approximieren. Wir schreiben \begin {equation} \Phi (x,y) \approx \Phi _N(x,y) = \sum _n a_n \varphi _n(x, y), \end {equation} wobei \(n\) ein eindeutiger Knotenindex ist. D.h. die Freiheitsgrade bzw. Expansionskoeffizienten \(a_n\) leben auf den Knoten (mit den Positionen \(\v {r}_n\)) des Simulationsgebietes, und für eine Finite-Elemente Basis wird wieder gelten \(\Phi (\v {r}_n)=a_n\), d.h. \(a_n\) ist der Funktionswert auf dem entsprechenden Knoten. Die Formfunktion ist dann eine Vorschrift, wie zwischen den Knoten (also über die Dreiecke) dieser Funktionswert interpoliert wird.
Anmerkung: In drei Dimensionen erfolgt die Zerlegung des Raumes üblicherweise in Tetraeder. Die Vernetzung eines solchen dreidimensionalen Gebiets ist höchst nicht-trivial. Alle kommerziellen Finite-Elemente Pakete haben Vernetzer eingebaut, die diesen Prozess übernehmen oder zumindest unterstützen. Eine freie Softwarelösung für die Vernetzung von komplexen Geometrien ist Gmsh (https://gmsh.info/).
10.2.2 Strukturierung
Die Nutzung eines strukturierten Gitters vereinfacht die Zuweisung eines Knotenindices \(n\) bzw. eines Elementindices \((n)\) zu entsprechenden räumlichen Positionen. Abbildung 10.3 zeigt eine solche strukturierte Zerlegung in \(M_x\times M_y\) (mit \(M_x=L_x/\Delta x=3\) und \(M_y=L_y/\Delta y=3\)) Kästen mit jeweils zwei Elementen. Das Gitter beinhaltet \(N_x \times N_y\) (mit \(N_x=M_x+1=4\) und \(N_y=M_y+1=4\)) Knoten.
In diesem strukturierten Gitter können wir von Koordinaten der Knoten auf deren globalen Index \(n_{\text {K}}\) schließen. Da die Freiheitsgrade auf den Knoten leben, identifiziert der globale Knotenindex \(n_{\text {K}}\) später eine Spalte oder Zeile aus der Systemmatrix. Sei \(i,j\) die (ganzzahlige) Koordinate des Knotens, dann ist \begin {equation} n_{\text {K}} = i + N_x j \label {eq:linindex} \end {equation} der entsprechende globale Knotenindex. Hierbei laufen die Knotenkoordinaten bei Null los, d.h. \(i\in \{0,1,\ldots ,N_x-1\}\) und \(j\in \{0,1,\ldots ,N_y-1\}\). Genauso können wir von Elementkoordinaten \(k,l,m\) auf den Elementindex \(n_{\text {E}}\) schließen, \begin {equation} n_{\text {E}} = k + 2(l + M_x m), \label {eq:linindexel} \end {equation} wobei nun \(l,m\) mit \(l\in \{0,1,\ldots ,M_x-1\}\) und \(m\in \{0,1,\ldots ,M_y-1\}\) die Koordinate des Kastens ist und \(k\in \{0, 1\}\) das Element innerhalb eines Kastens indiziert. Der Faktor \(2\) taucht in Gl. \eqref{eq:linindexel} auf, weil es zwei Elemente pro Kasten gibt.
Anmerkung: Gleichungen \eqref{eq:linindex} und \eqref{eq:linindexel} sind die vermutlich einfachste Abbildung von Koordinaten auf einen linearen, konsekutiven Index. Andere Möglichkeiten, die auch in der Numerik eingesetzt werden, ergeben sich durch die raumfüllenden Kurven, wie z.B. die Hilbert- oder Peano-Kurve. Raumfüllende Kurven haben teilweise vorteilhafte Eigenschaften, wie z.B. dass Koordinaten die nah beieinander liegen auch Indices bekommen, die nah bei einander liegen. Dies führt zu einer kompakteren Struktur der dünnbesetzten Systemmatrix und kann Vorteile in der Laufzeit der Algorithmen mit sich bringen. Der Grund für solche Laufzeitvorteile ist eng mit der Hardware verknüpft, z.B. wie die Hardware Speicherzugriff organisiert und Caches nutzt. Eine Optimierung von Algorithmen für spezifische Hardwarearchitekturen ist höcht nicht-trivial und benötigt detailliertes Wissen über die Rechnerarchitektur.
10.3 Formfunktionen
Unsere Formfunktionen leben auf den einzelnen Dreiecken der Triangulierung und müssen auf den jeweiligen Knoten entweder \(1\) sein oder verschwinden. Wir drücken die Formfunktionen hier mit Hilfe der skalierten Koordinaten \(\xi =(x-x_0)/\Delta x\) und \(\eta =(y-y_0)/\Delta y\) aus, wobei \(x_0\) und \(y_0\) der Ursprung des jeweiligen Kastens ist. Damit ist in der linken unteren Ecke des Kastens \(\xi =0\) und \(\eta =0\) und in der rechten obere Ecke \(\xi =1\) und \(\eta =1\).
Die Formfunktionen für das Element mit lokalen Elementindex \((0)\) (siehe Abb. 10.3b) lauten \begin {align} N^{(0)}_0(\xi , \eta ) &= 1-\xi -\eta \\ \label {eq:formfunc1} N^{(0)}_1(\xi , \eta ) &= \xi \\ N^{(0)}_2(\xi , \eta ) &= \eta , \end {align}
wobei der Index \(i\) in \(N^{(0)}_i\) den lokalen Knotenindex bezeichnet, bei dem die Formfunktion \(1\) wird. Diese Formfunktionen sind in Abb. 10.4 gezeigt. Auf Element \((1)\) lauten die Formfunktionen \begin {align} N^{(1)}_0(\xi , \eta ) &= \xi +\eta -1 \\ N^{(1)}_1(\xi , \eta ) &= 1-\xi \\ \label {eq:formfunc6} N^{(1)}_2(\xi , \eta ) &= 1-\eta . \end {align}
Diese Formfunktionen erfüllen die Eigenschaft \(N^{(n)}_0+N^{(n)}_1+N^{(n)}_2=1\), die sich Zerlegung der Eins (engl. “partition of unity”) nennt.
Wir brauchen im folgenden die Ableitungen der Formfunktionen respektive der Positionen \(x\) und \(y\). Im allgemeinen Fall erhält man \begin {align} \frac {\partial N_i^{(n)}}{\partial x} &= \frac {\partial N_i^{(n)}}{\partial \xi } \frac {\partial \xi }{\partial x} + \frac {\partial N_i^{(n)}}{\partial \eta } \frac {\partial \eta }{\partial x} \\ \frac {\partial N_i^{(n)}}{\partial y} &= \frac {\partial N_i^{(n)}}{\partial \xi } \frac {\partial \xi }{\partial y} + \frac {\partial N_i^{(n)}}{\partial \eta } \frac {\partial \eta }{\partial y}, \end {align}
oder in kompakter Matrix-Vektor Schreibweise \begin {equation} \nabla _{x,y} N_i^{(n)}\cdot \t {J} = \nabla _{\xi ,\eta } N_i^{(n)}, \label {eq:formgrad} \end {equation} wobei \(\nabla _{x,y}\) den Gradienten respektive der angezeigten Koordinaten meint. Die Matrix \begin {equation} \t {J} = \begin {pmatrix} \partial x/\partial \xi & \partial x/\partial \eta \\ \partial y/\partial \xi & \partial y/\partial \eta \end {pmatrix} = \begin {pmatrix} \Delta x & 0 \\ 0 & \Delta y \end {pmatrix} \label {eq:jacobi} \end {equation} nennt sich Jacobi-Matrix. In unserem Beispiel ergibt sich die explizite Matrix auf der rechten Seite von Gl. \eqref{eq:jacobi}, die unabhängig vom Kasten ist, den wir betrachten. Für komplexere Gitter (z.B. Abb. 10.2b) beschreibt die Jacobi-Matrix die Form der Dreiecke und damit die Struktur des Gitters. Die Darstellung mit Hilfe der reskalierten Koordinaten \(\xi \) und \(\eta \), und damit Gl. \eqref{eq:formgrad} als Gradienten, entkoppelt die Interpolationsvorschrift Gl. \eqref{eq:formfunc1}-\eqref{eq:formfunc6} von der Struktur des Gitters und ist daher besonders für unstrukturierte Gitter nützlich.
Für unser Gitter finden wir also \begin {align} \frac {\partial N_0^{(0)}}{\partial x} &= -1/\Delta x,\quad \frac {\partial N_0^{(0)}}{\partial y} = -1/\Delta y, \\ \frac {\partial N_1^{(0)}}{\partial x} &= 1/\Delta x,\quad \frac {\partial N_1^{(0)}}{\partial y} = 0, \\ \frac {\partial N_2^{(0)}}{\partial x} &= 0,\quad \frac {\partial N_2^{(0)}}{\partial y} = 1/\Delta y, \\ \frac {\partial N_0^{(1)}}{\partial x} &= 1/\Delta x,\quad \frac {\partial N_0^{(1)}}{\partial y} = 1/\Delta y, \label {eq:N10der} \\ \frac {\partial N_1^{(1)}}{\partial x} &= -1/\Delta x,\quad \frac {\partial N_1^{(1)}}{\partial y} = 0, \\ \frac {\partial N_2^{(1)}}{\partial x} &= 0,\quad \frac {\partial N_2^{(1)}}{\partial y} = -1/\Delta y \label {eq:N12der} \end {align}
für die Ableitungen der Formfunktionen. Da wir lediglich lineare Elemente verwandt haben, sind diese Ableitungen alle Konstanten.
10.4 Galerkin-Methode
Wir können nun die Galerkin-Methode anwenden, um das lineare Gleichungssystem, welches die diskretisierte Differentialgleichung beschreibt, zu bestimmen. Wir unterscheiden hier wieder zwischen Elementmatrizen und der Systemmatrix. Für die Elementmatrix schreiben wir den Beitrag der Formfunktion zur Galerkin-Bedingung auf. Man erhält \begin {equation} \begin {split} (N_I^{(n)}, R) &= \left (N_I^{(n)}, \nabla ^2 \Phi + \frac {\rho (\v {r})}{\varepsilon }\right ) \\ &= \int _{\partial \Omega } \dif ^2r\, N_I^{(n)}(\v {r})\nabla \Phi \cdot \hat {n}(\v {r}) - \sum _J a_J (\nabla N_I^{(n)}, \nabla N_J^{(n)}) + \frac {1}{\varepsilon } (N_I^{(n)}, \rho ), \\ &= - \sum _J K_{IJ}^{(n)} a_J + f_I^{(n)}, \end {split} \end {equation} wobei \(K_{IJ}^{(n)}\) nun die Elementmatrix ist und \(f_I^{(n)}\) der Beitrag des Elements zur rechten Seite. Man erhält \begin {equation} K_{IJ}^{(n)} = (\nabla N_I^{(n)}, \nabla N_J^{(n)}). \end {equation} wobei für zwei Vektorfelder \(\v {f}(\v {r})\) und \(\v {g}(\v {r})\) das Skalarprodukt als \begin {equation} (\v {f}, \v {g}) = \int _\Omega \dif ^3r\, \v {f}^*(\v {r})\cdot \v {g}(\v {r}), \end {equation} also als kartesisches Skalarprodukt zwischen den beiden Funktionswerten, zu verstehen ist. Der Beitrag des Elements zur rechten Seite lautet \begin {equation} f_I^{(n)} = \frac {1}{\varepsilon }(N_I^{(n)}, \rho ) + \int _{\partial \Omega } \dif ^2r\, N_I^{(n)}(\v {r})\nabla \Phi \cdot \hat {n}(\v {r}). \label {eq:rhs2d} \end {equation}
Beispiel: Wir berechnen nun die Elementmatrizen für die beiden Elemente unseres strukturierten Beispielgitters. So lautet z.B. die Komponente \(I=0\) und \(J=0\) des Elements \((0)\), \begin {equation} \begin {split} K_{00}^{(0)} &= (\nabla N_0^{(0)}, \nabla N_0^{(0)}) \\ &= \int _{\Omega ^{(0)}} \dif ^2r \left ( \frac {1}{\Delta x^2} + \frac {1}{\Delta y^2} \right ) \\ &= \frac {\Delta x\Delta y}{2} \left ( \frac {1}{\Delta x^2} + \frac {1}{\Delta y^2} \right ) \\ &= \frac {1}{2}\left (\frac {\Delta y}{\Delta x} + \frac {\Delta x}{\Delta y}\right ) \end {split} \end {equation} wobei der Faktor \(\Delta x\Delta y/2\) die Fläche des Elements ist. Wir betrachten im folgenden den Spezialfall \(\Delta x=\Delta y\), in dem man \(K_{00}^{(0)}=1\) erhält. (Im eindimensionalen Fall blieb hier noch ein \(1/\Delta x\) stehen. Die Einheiten von \(K\) unterscheiden sich damit im eindimensionalen und zweidimensionalen Fall!)
Die andere Skalarprodukte können ähnlich ausgerechnet werden. Man erhält \begin {equation} \t {K}^{(0)} = \t {K}^{(1)} = \begin {pmatrix} 1 & -1/2 & -1/2 \\ -1/2 & 1/2 & 0 \\ -1/2 & 0 & 1/2 \end {pmatrix} \label {eq:elmat2d} \end {equation} für beide Elementmatrizen. Diese Matrizen sind identisch, weil die Nummerierung der lokalen Elementknoten so gewählt wurde, dass die beiden Dreiecke ineinander rotiert werden können (siehe Abb. 10.3b).
Aus diesen Elementmatrizen müssen wir nun die Systemmatrix zusammenbauen. Die lokalen Knotenindices sind in Abb. 10.3b gezeigt. Diese entsprechen den Spalten und Zeilen von Gl. \eqref{eq:elmat2d}. Sie müssen nun auf die globalen Knotenindices abgebildet werden und in der Systemmatrix summiert werden. So müssen wir Beispielsweise für Element \((8)\) in Abb. 10.3a den lokalen Knoten \(0\) auf den globalen Knoten \(5\) abbilden, \(0\to 5\). D.h. die erste Zeile der Elementmatrix wird zur sechsten Zeile der Systemmatrix. (Es ist die sechste Zeile, und nicht die fünfte Zeile, da die Indizierung bei Null beginnt.) Weiterhin müssen wir \(1\to 6\) und \(2\to 9\) abbilden. Der Beitrag \(\Delta \t {K}^{(8)}\) von Element \((8)\) zur \(16\times 16\) Systemmatrix ist daher \begin {equation} \Delta \t {K}^{(8)} = \left (\begin {array}{*{16}c} \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & 1 & -\frac {1}{2} & \cdot & \cdot & -\frac {1}{2} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & -\frac {1}{2} & \frac {1}{2} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & -\frac {1}{2} & \cdot & \cdot & \cdot & \frac {1}{2} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \end {array}\right ) \label {eq:elmat2dlarge} \end {equation} wobei Enträge mit Wert \(0\) zur besseren visuellen Darstellung als Punkt (\(\cdot \)) gezeigt sind. Die gesamte Systemmatrix ergibt sich dann als Summe über alle Elemente, \(\t {K}=\sum _n \t {K}^{(n)}\). Man erhält \begin {equation} \t {K} = \left (\begin {array}{*{16}c} 1 & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \bar {\frac {1}{2}} & 1 & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & 2 & \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & 2 & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & 2 & \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {1} & 4 & \bar {1} & \cdot & \cdot & \bar {1} & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {1} & 2 & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \cdot & 1 & \bar {\frac {1}{2}} & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {1} & \cdot & \cdot & \bar {\frac {1}{2}} & 2 & \bar {\frac {1}{2}} \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \bar {\frac {1}{2}} & \cdot & \cdot & \bar {\frac {1}{2}} & 1 \end {array}\right ) \label {eq:sysmat2d} \end {equation} wobei der Balken über der Zahl ein Minus anzeigt, also z.B. \(\bar {1}=-1\). Diese \(16\times 16\) Matrix ist wiederum nicht regulär; ihr Rang ist 15. D.h. man braucht mindestens eine Dirichlet-Randbedingung, um zu einem lösbaren Problem zu kommen. Anhand dieses Beispiels wird auch vermutlich klar, dass die Systemmatrix nur schwer von Hand auszurechnen ist und wir einen Computer zu Hilfe ziehen müssen.
10.5 Randbedingungen
10.5.1 Dirichlet-Randbedingungen
Dirichlet-Randbedingungen funktionieren in höheren Dimensionen analog zum eindimensionalen Fall. Wir fixieren den Funktionswert auf einem Knoten. Man erhält \(\Phi _N(\v {r}_n)=a_n\equiv \Phi _n\), wobei \(\Phi _n\) der gewählte Funktionswert ist, und ersetzt damit eine Galerkin-Bedingung durch diese Fixierung des Potential auf den Knoten.
10.5.2 Neumann-Randbedingungen
Wie im eindimensionalen Fall werden Neumann-Randbedingungen über den Oberflächenterm in Gl. \eqref{eq:rhs2d} in die rechte Seite eingebaut. Diese Bedingungen werden daher auf den Seiten der Dreiecke definiert. Für eine konstanten Richtungsableitung \(\Phi ^\prime = \nabla \Phi \cdot \hat {n}\) erhält man \begin {equation} f_I^{(n)} = \frac {1}{\varepsilon }(N_I^{(n)}, \rho ) + \Phi ^\prime \int _{\partial \Omega } \dif r\, N_I^{(n)}(\v {r}). \label {eq:rhs2d2} \end {equation} Das Integral in Gl. \eqref{eq:rhs2d2} wird über die Seite des Dreiecks ausgeführt. Für die Seite zwischen den Knoten \(2\) und \(3\) (siehe Abb. 10.3), beispielsweise, sind die Formfunktionen \(N_0^{(0)}\) und \(N_1^{(0)}\) (Element \((4)\)) ungleich Null. Man erhält \begin {align} f_0^{(4)} &= \frac {1}{\varepsilon }(N_0^{(0)}, \rho ) + \Phi ^\prime \int _0^{\Delta x} \dif x\, (1-x/\Delta x) = \frac {1}{\varepsilon }(N_0^{(0)}, \rho ) + \frac {1}{2}\Phi ^\prime \Delta x \\ f_1^{(4)} &= \frac {1}{\varepsilon }(N_1^{(0)}, \rho ) + \Phi ^\prime \int _0^{\Delta x} \dif x\, x/\Delta x = \frac {1}{\varepsilon }(N_1^{(0)}, \rho ) + \frac {1}{2}\Phi ^\prime \Delta x \end {align}
für die rechte Seite. Die Randbedingungen, welche man ohne weitere Modifikation der rechten Seite erhält (siehe Gl. \eqref{eq:sysmat2d}), sind daher Neumann-Bedingungen mit verschwindender Ableitung, \(\Phi ^\prime = 0\).